VAR(ベクトル自己回帰)モデルを用いた多変量時系列データ分析
日経平均株価(NIKKEI225)はS&P500と相関があることはよく知られた話である。
今回、多変量の時系列データ分析を扱う際に使用されるVAR(ベクトル自己回帰)モデルを使用してNIKKEI225とS&P500の関係性(因果探索)の分析を行なってみる。 ベクトル自己回帰(VAR)モデルは、自己回帰(AR)モデルを多変量に拡張したものである。互いに相関する複数の時系列データを分析する際に使用する。 ここで、 つまり、自己相関を持たず、異時点で系列データ間でも相関を持たない。ただ、同一時点では相関を許容する。( 前説で簡単に説明したが、ここではもう少しだけ詳しく説明する。 この時、 手順としては、はじめに、VARモデルにおける ここで, ある変数時系列の変化がその変数時系列やその他の変数時系列に与える影響を分析することができるのが、インパルス応答関数である。変化の識別の仕方によって、複数のインパルス応答関数が存在し、直行化インパルス応答関数と非直行化インパルス応答関数とがある。 非直行化インパルス応答解析 直行化インパルス応答解析 それでは、Pythonのstatsmodelライブラリを使用してVARモデルの構築からグレンジャー因果性の統計的仮説検定、インパルス応答解析をおこなってみる。今回は冒頭に書いたようにNIKKEI225とS&P500の関係性を分析してみる。 pandas_datareaderモジュールを使用してNIKKEI225、S&P500のデータを取得した。 取得したデータを描画してみる。 相関がありそうなことが確認できる。
上図から明らかなように両系列データともに定常性を満たしていない。一応ADF検定により定常性を確認してみる。 仮に有意水準5%と仮定した場合、両系列データの検定値は0.05より大きく定常性が認められない。 上記結果から定常性が認められなかったので、そのままのデータでは定常性を前提とするVARモデルによるモデル化ができない。 対数差分処理を行うことで前の時刻からの変化率に変換できる。変化分が小さいと仮定すると、一次のテイラー展開近似により変化率に変換ができる。今回はこれに100をかけることで割合にしておく。 対数差分処理後のデータを描画してみる。 定常データになっていそうなことが確認できる。 再度ADF検定を行い、定常性の確認を行う。 定常な系列データに変換することができた。一度データフレーム形式で両系列データをまとめておく。 いよいよVAR(ベクトル自己回帰モデル)を構築し、グレンジャー因果性に関する統計的仮説検定、インパルス応答解析を行なっていく。
その前に相互相関を確認しておく。 相互相関コレログラムは以下のようになり、0期(同一時点)と1期ずれた点で相関が高いことが確認できる。
statsmodelsライブラリのtsa.vector_ar.var_model を使用することでVARモデルの推定が行える。今回は最大となるラグを指定し、ベイズ情報量(BIC)を基準にラグを最適化し、最適化したラグでVARモデルの推定を行った。 ベイズ情報量基準(BIC)による最適なラグ探索結果と最適なラグで学習させた時のVARモデルのサマリーが出力される。
また最後に量系列データの相関行列が表示される。 モデルサマリーをみると、NIKKEI225の予測に関しては、1日前のNIKKEI225と1日前、2日前のS&P500の値を使用することは優位であることがわかる。(有意水準5%の場合) 一方、S&P500の予測に関しては、1日前と2日前のS&P500の値を使用することは統計的に優位であるが、NIKKEI225の値は優位でないと分かる。つまり、NIKKEI225はS&P500の影響を受けるが、S&P500はNIKKEI225の影響をほぼ受けないことが分かる。 そのため、グレンジャー因果性的には、S%P500→NIKKEI225の向きに因果があると想定されます。 続いて推定したVARモデルでグレンジャー因果性の統計的仮説検定を行う。以下のコードで実行できる。 検定結果は以下の通りである。SP500 -> NIKKEI225の方向の因果は統計的に優位であることが確認でき、NIKKEI250を予測するのにS&P500は有効であることが確認できる。 インパルス応答関数は、statsmodelsモジュールを使えば簡単に実行できる。インパルス応答関数は、非直交化と直交化の2種類あり、plotのorth引数で切り替えることができる。orthをTrueにすると直交化された結果が表示される。まず非直行化インパルス応答解析を行なってみる。 5期先の影響までを描画する。 上記のインパルス応答解析結果から、S&P500に1単位のショックを与えた1日後に大きくNIKKEI225の値が増えていることが分かる。一方でNIKKEI225に1単位分のショックを与えた場合に正の方向への変化は見られない。インパルス応答解析結果は、VARモデルサマリーやグレンジャー因果性の検定結果と同等の分析結果を示唆した。 非直行化インパルス応答解析を行う場合、1単位分(今回は1%変化分)のショックを撹乱項に与えた場合の結果になる。外乱項の1偏差分のショックを与えた場合の影響を定量的に把握したい場合は、以下で求められる外乱項の偏差を応答値に書けることで確認できる。 それぞれの撹乱項の偏差は以下である。 ちなみにインパルス応答解析の生データは 続いて直行化インパルス応答解析を行う。 非直行化インパルス応答解析では現れていなかったNIKKEI225→S&P500の0期での影響が大きく出ていることが確認できる。直行化することでNIKKEI225にショックを与えたことでそれと相関する撹乱項が同じ時点のS&P500にも与えられるために0期の値が大きくなったと考えられる。
また、直行化インパルス応答解析では、1偏差分のショックが与えられた場合の結果がでてくる。この際の標準偏差は下記で導出できる。 今回のケースでは、下記のようになり、ショックとしてNIKKEI225に1%増加を与えた場合、S&P500に1.05%の増加を与えた場合の結果がインパルス応答解析結果として描画されていることになる。 ここでもう少しだけインパルス応答解析結果に関して、考察しておく。S&P500→NIKKEI225の0期の影響が0になっているが、これは日本と米国の株式市場の開いてる時間に起因する。米国市場は日本市場が閉まった後に開くため、同一期(同じ日)にS&P500→NIKKEI225に影響(インパルス)があるはずがない。これが反映されているために0になっていると考えられる。 市場の開閉の順番を誤ったように並べてインパルス応答解析を行うと、同時点のS&P500がNIKKEI225に影響を与える(本来1期前のS&P500がNIKKEI225に影響を与えるはず)という結果が得られてしまう。インパるす応答解析では変数の順序を正しく設定することが結果を解釈する上で重要である。

1.やりたいこと
2.VAR(ベクトル自己回帰)モデル
VARモデルは以下の式で示めされるように過去のp期前までの各系列データの値を使用して現時点の各系列データの値を予測しようとするモデルである。
はベクトルホワイトノイズ(撹乱項)であり、以下の式を満たす。
を分散分散行列とする。)
VARモデルの推定は、撹乱項を多変量正規分布に従うとするなどして、各系列データに関する方程式を個別にOLSすることによって推定していく。
VARモデル解析においては、グレンジャー因果性、インパルス応答解析、分散分解という3つのツールが重要な役割を果たす。ここではグレンジャー因果性とインパルス応答解析を扱う。
グレンジャー因果性はある変数(群)が他の変数(群)の予測の向上に役立つかどうか判定するものであり、インパルス応答解析はある変数に対するショックがその変数やその他の変数の値に与える影響を分析するものである。
グレンジャー因果性やインパルス応答解析を行うことで系列データ間の因果関係の探索、予測精度向上に重要なラグや変数の特定および変数の影響度を把握することが可能になります。例えば、目的変数yに異常が生じた場合に系列データ間の関連性(因果関係)を把握できていれば、原因の特定につながる。また、影響にラグがある場合にどの程度影響が残存してしまうのかは多変量の系列データを制御する場合に重要な情報となる。3.グレンジャー因果性
基本的な考え方は、時系列の予測において、時系列
を用いると予測精度が向上した場合、
から
への因果性があるという考え方である。
ここで、2変量VAR(2)モデルについて考える。
から
へのグレンジャー因果性が存在している場合、
と同値になる。
逆にグレンジャー因果性がない場合は、係数が全て0であると同値になる。
そのため、グレンジャー因果性を検定するためには,F検定を用いて
を検定し求めていく。
のモデルをOLSで推定し、その残差平方を
とする。
次に、VARモデルにおける
のモデルに制約を貸したモデルをOLSで推定し、その残差平方を
とする。
F統計量を次のように算出します。
はグレンジャー因果性検定に必要な制約数である。
そして、
を
の95%点と比較し、
の方が大きければ、ある変数群からの
へのグレンジャー因果性は存在し、小さければグレンジャー因果性は存在しないと結論付ける。
グレンジャー因果性はグレンジャー因果性は通常の因果性とは異なることに注意したい。グレンジャー因果性は通常の因果性が存在する必要条件ではあるが、十分条件ではない。
また、因果の方向が実際と真逆になることもある。そのため因果の方向がはっきりしている場合をのぞいて、定義通りに予測に優位かどうかという観点で解釈するのが良いとされている。
4.インパルス応答解析
の撹乱項
だけに1単位(または1標準偏差)のショックを与えたときの
の変化は、
のショックに対する
の
期後の非直交化インパルス応答と呼ばれる。また、それを
の関数としてみたものは、
のショックに対する
の非直交化インパルス応答関数といわれる。
撹乱項の分散共分散行列の三角分解を用いて、撹乱項を互いに相関する部分と無相関な部分に分解したとき、無相関な部分は直交化撹乱項といわれる。また、の直交化撹乱項に1単位または1標準偏差のショックを与えたときの
の直交化インパルス応答を時間の関数としてみたものは、
に対する
の直交化インパルス応答関数といわれる。
5.NIKKEI225とS&P500の因果探索(Pythonでの実装)
5.1.データの用意
import pandas_datareader.data as web
import datetime
#2013年10月10日を収集開始時点にする
start =datetime.date(2013,10,10)
#2023年9月30日を収集終了時点にする
end = datetime.date(2023,9, 30)
df_nikkei = web.DataReader('NIKKEI225', 'fred', start, end)
df_sp500 = web.DataReader('SP500', 'fred', start, end)
#データがない日付を特定
drop_ind_nikkei = df_nikkei[df_nikkei['NIKKEI225'].isnull() == True].index
drop_ind_sp500 = df_sp500[df_sp500['SP500'].isnull() == True].index
drop_ind = drop_ind_nikkei.append(drop_ind_sp500)
#データがない日付を削除
df_nikkei = df_nikkei.drop(drop_ind)
df_sp500 = df_sp500.drop(drop_ind)
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(16, 8))
ax1 = fig.add_subplot(2, 1, 1)
ax1.plot(df_nikkei.index, df_nikkei['NIKKEI225'])
ax1.set_title('NIKKEI225')
ax2 = fig.add_subplot(2, 1, 2)
ax2.plot(df_sp500.index, df_sp500['SP500'])
ax2.set_title('S&P500')
plt.show()

5.2.定常性の確認
import statsmodels.api as sm
from statsmodels.tsa.stattools import adfuller
#ADF検定(単位根検定、元データ)
c_results = adfuller(df_nikkei['NIKKEI225'], regression='c')
print('NIKKEI225:', c_results[1])
c_results = adfuller(df_sp500['SP500'], regression='c')
print('SP500:', c_results[1])
NIKKEI225: 0.7150331280648695
SP500: 0.873103776458502
この問題に対処するため、対数差分処理を行う。一般に下記に示すような対数差分処理や差分処理を行うことで定常になるように変換する。
#対数差分をとって変化率に変換する処理
import numpy as np
#時系列データにおける対数差分は、前期からの比率を表すので、このあとの結果がわかりやすくなるように100をかけています。
df_nikkei_log = np.log(df_nikkei['NIKKEI225']).diff(1)*100
df_nikkei_log = df_nikkei_log[1:]
df_sp500_log = np.log(df_sp500['SP500']).diff(1)*100
df_sp500_log = df_sp500_log[1:]
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(16, 8))
ax1 = fig.add_subplot(2, 1, 1)
ax1.plot(df_nikkei.index[1:], df_nikkei_log)
ax1.set_title('NIKKEI225')
ax1.set_ylim(-10, 10)
ax2 = fig.add_subplot(2, 1, 2)
ax2.plot(df_sp500.index[1:], df_sp500_log)
ax2.set_title('S&P500')
ax2.set_ylim(-10, 10)
plt.show()

#ADF検定(単位根検定、対数差分)
c_results = adfuller(df_nikkei_log, regression='c')
print('NIKKEI225:', c_results[1])
c_results = adfuller(df_sp500_log, regression='c')
print('SP500:', c_results[1])
NIKKEI225: 0.0
SP500: 6.1407766905440326e-21
df_nikkei_log = pd.DataFrame(df_nikkei_log, columns=['NIKKEI225'])
df_sp500_log = pd.DataFrame(df_sp500_log, columns=['SP500'])
df = pd.concat([df_nikkei_log, df_sp500_log], axis=1)
#相互相関コレログラム
fig = plt.figure(figsize=(16, 2))
plt.xcorr(df['NIKKEI225'], df['SP500'])
plt.title('NIKKEI225*S&P500')
plt.show()

5.3.VARモデルの構築
# VARモデルの構築
from statsmodels.tsa.vector_ar.var_model import VAR
# 最大のラグ数
maxlags = 10
# モデルのインスタンス生成
var_model = VAR(df)
# 最適なラグの探索
# ベイズ情報量基準で最適なラグを決定する
lag = var_model.select_order(maxlags).selected_orders
print('最適なラグ:',lag['bic'],'\n')
# モデルの学習
# 最適なラグでVARモデルを学習させる
results = var_model.fit(lag['bic'])
# 結果出力
print(results.summary())
最適なラグ: 2
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Mon, 16, Oct, 2023
Time: 17:44:44
--------------------------------------------------------------------
No. of Equations: 2.00000 BIC: 0.427853
Nobs: 2350.00 HQIC: 0.412263
Log likelihood: -7132.93 FPE: 1.49680
AIC: 0.403333 Det(Omega_mle): 1.49046
--------------------------------------------------------------------
Results for equation NIKKEI225
===============================================================================
coefficient std. error t-stat prob
-------------------------------------------------------------------------------
const 0.011922 0.023616 0.505 0.614
L1.NIKKEI225 -0.203864 0.021595 -9.440 0.000
L1.SP500 0.543548 0.022090 24.606 0.000
L2.NIKKEI225 -0.002393 0.019161 -0.125 0.901
L2.SP500 0.180303 0.024491 7.362 0.000
===============================================================================
Results for equation SP500
===============================================================================
coefficient std. error t-stat prob
-------------------------------------------------------------------------------
const 0.040638 0.023308 1.744 0.081
L1.NIKKEI225 0.027808 0.021313 1.305 0.192
L1.SP500 -0.144626 0.021802 -6.634 0.000
L2.NIKKEI225 -0.019569 0.018911 -1.035 0.301
L2.SP500 0.083522 0.024172 3.455 0.001
===============================================================================
Correlation matrix of residuals
NIKKEI225 SP500
NIKKEI225 1.000000 0.322193
SP500 0.322193 1.000000
Results for equation NIKKEI225
===============================================================================
coefficient std. error t-stat prob
-------------------------------------------------------------------------------
const 0.011922 0.023616 0.505 0.614
L1.NIKKEI225 -0.203864 0.021595 -9.440 0.000
L1.SP500 0.543548 0.022090 24.606 0.000
L2.NIKKEI225 -0.002393 0.019161 -0.125 0.901
L2.SP500 0.180303 0.024491 7.362 0.000
===============================================================================
Results for equation SP500
===============================================================================
coefficient std. error t-stat prob
-------------------------------------------------------------------------------
const 0.040638 0.023308 1.744 0.081
L1.NIKKEI225 0.027808 0.021313 1.305 0.192
L1.SP500 -0.144626 0.021802 -6.634 0.000
L2.NIKKEI225 -0.019569 0.018911 -1.035 0.301
L2.SP500 0.083522 0.024172 3.455 0.001
===============================================================================
5.4.グレンジャー因果性の統計的仮説検定
# グレンジャー因果性の検定
# 帰無仮説:グレンジャー因果なし
# 対立仮説:グレンジャー因果あり
for i in range(len(df.columns)):
for j in range(len(df.columns)):
if i != j :
#因果の検定
test_results = results.test_causality(causing=i, caused=j)
#p値
test_results.pvalue
#検定結果の出力
print(df.columns[i],'->',df.columns[j],'\t',test_results.pvalue)
NIKKEI225 -> SP500 0.19007514052849195
SP500 -> NIKKEI225 2.227002166652272e-124
5.5.インパルス応答解析
5.5.1 非直行化インパルス応答解析
# インパルス応答関数(直交化)
irf = results.irf(5)
irf.plot(orth=False)
plt.show()

print("ε_NIKKEI225:",np.sqrt(results.sigma_u['NIKKEI225']['NIKKEI225']))
print("ε_S&P500:",np.sqrt(results.sigma_u['SP500']['SP500']))
ε_NIKKEI225 1.1430889085971325
ε_S&P500 1.1281818499705119
irf.irfsで取得できるので、1偏差のショックを与えた時のインパルス応答解析結果のプロットも可能である。fig = plt.figure(figsize=(12, 12))
#NIKKEI225→NIKKEI225
ax1 = fig.add_subplot(2,2,1)
ax1.plot(irf.irfs[:, 0, 0]*np.sqrt(results.sigma_u['NIKKEI225']['NIKKEI225']))
ax1.set_title('NIKKEI225→NIKKEI225')
#SP500→NIKKEI225
ax2 = fig.add_subplot(2,2,2)
ax2.plot(irf.irfs[:, 0, 1]*np.sqrt(results.sigma_u['SP500']['SP500']))
ax2.set_title('SP500→NIKKEI225')
#NIKKEI225→SP500
ax3 = fig.add_subplot(2,2,3)
ax3.plot(irf.irfs[:, 1, 0]*np.sqrt(results.sigma_u['NIKKEI225']['NIKKEI225']))
ax3.set_title('NIKKEI225→SP500')
#SP500→SP500
ax4 = fig.add_subplot(2,2,4)
ax4.plot(irf.irfs[:, 1, 1]*np.sqrt(results.sigma_u['SP500']['SP500']))
ax4.set_title('SP500→SP500')
plt.show()

5.5.2 直行化インパルス応答解析
# インパルス応答関数(直交化)
irf = results.irf(5)
irf.plot(orth=True)
plt.show()

sigma = results.sigma_u
L = np.linalg.cholesky(sigma)
L_inv = np.linalg.inv(L)
L_t_inv = np.linalg.inv(L.T)
D = L_inv * sigma * L_t_inv
new_sigma_sqrt = np.sqrt(np.diag(D))
new_sigma_sqrt
array([1. , 1.05632992])
また、インパルス応答解析では系列データの並びが重要である。今回は市場が開く順番(日本→米国)でデータを並べたが、並びが変わるとインパルス応答解析結果も変わってしまう。仮にS&P500→NIKKEI225に並びを変えてインパルス応答解析を行なってみると、以下のようになる。
#VARモデル作成時にNIKKEI225とS&P500の並びを変えるとインパルス応答解析の結果が変わる。
df = pd.concat([df_sp500_log, df_nikkei_log], axis=1)
# VARモデルの構築
from statsmodels.tsa.vector_ar.var_model import VAR
# 最大のラグ数
maxlags = 10
# モデルのインスタンス生成
var_model = VAR(df)
# 最適なラグの探索
# ベイズ情報量基準で最適なラグを決定する
lag = var_model.select_order(maxlags).selected_orders
print('最適なラグ:',lag['bic'],'\n')
# モデルの学習
# 最適なラグでVARモデルを学習させる
results = var_model.fit(lag['bic'])
# インパルス応答関数(直交化)
irf = results.irf(5)
irf.plot(orth=True)
plt.show()

6.参考
VARモデル構築やグレンジャー因果性の統計的仮説検定、インパルス応答解析の実装はこちらの本を参考にさせて頂いた。
BERTで感情予測をしてみる
 https://arxiv.org/pdf/1810.04805.pdf
https://arxiv.org/pdf/1810.04805.pdf
0.目次
- 0.目次
- 1.やりたいこと
- 2.BERT(Bidirectional Encoder Representation from Transformers)
- 3.Transformersライブラリ
- 4.使用するデータセット
- 5.学習済みBERTを使用した感情分析モデルの構築(ファインチューニング)
- 6.参考文献
1.やりたいこと
最近流行のChatGPT等のLLM(Large Language Model)について勉強していると、Hugging face社の学習済みLLMを使って簡単にファインチューニングをして個々のタスクに適用できることを知りました。今回は、学習済みBERT(Bidirectional Encoder Representation from Transformers)ファインチューニングして人間の感情分類するモデルを構築してみます。
2.BERT(Bidirectional Encoder Representation from Transformers)
BERTは、2018年にGoogleによって発表され、NLPタスクにおける驚異的な性能向上をもたらしました。Transformersモデルのエンコーダ部分だけを使用したNLPモデルです。 詳しくは以下のBERTの論文を参照ください。
https://arxiv.org/pdf/1810.04805.pdf
2.1.BERTの事前学習
私たちがLLMを使用する際に1からモデルを学習させることはほとんどありません。BERTでは大規模な文章を用いて汎用的な言語パターンを事前にモデルに学習させておき(事前学習)、個々のタスクに合わせてモデルをチューニングしていきます。
BERTではMasked Language ModelとNext Sentence Predictionという2つの方法を組み合わせて大量のデータから学習を行なっていきます。
Masked Language Model
テキストの一部をマスクして前後の文章からマスク部分の単語を予測します。前後の文脈からマスク部分を予測できるように学習させます。
Next Sentence Prediction
2つの文を入力して2つの文章の関係性について予測します。2つの分の関係性を見分けられるように学習させます。
2.2.BERTのファインチューニング
BERTで個別のタスクを解くためには、タスクの内容に応じてBERTに新しい分類機などを接続するなどして、タスクに特化したモデルを作ります。事前学習の結果、出力層側では大量の文章の文脈に沿って動的に重み付けされたテキストのベクトル値が得られます。個別のタスクに応じてモデルをチューニングさせ、より個別のタスクに有利なようにこのベクトル値を調整していきます。ファインチューニングの際事前学習で得られたパラメータを初期値として用いることで比較的少数の学習データでも高い性能のモデルを得られます。
3.Transformersライブラリ
今回アメリカのHugging face社が提供するTransformersライブラリを使用します。テキスト要約、分類、生成等の様々な自然言語処理モデルを提供しており、事前学習モデルを使用することで簡単に個別のタスクに応じたファインチューニングが可能です。 詳しくは以下のリンクを参照ください。
4.使用するデータセット
今回の感情分析モデルを構築するにあたり以下のデータを使用します。
www.kaggle.com
使用するデータはテキストと感情ラベルで構成されています。
'anger', 'disgust', 'fear', 'guilt', 'joy', 'sadness', 'shame'と7つの感情ラベルがありますが、今回は'joy'なのか'anger'なのかを判別する二値分類モデルを構築したいと思います。


5.学習済みBERTを使用した感情分析モデルの構築(ファインチューニング)
Google Colaboratoryを使用して行います。
5.1.ライブラリのインストール
!pip install transformers==4.26.0 !pip install datasets
Huggingface社のBERT等のLLMモデルを使用することができるライブラリTransformersをインストールします。 加えて、同じくHuggingface社のdatasetsモジュールをインストールしておきます。このモジュールを使用することでpandas.DataFrame形式で読み込んだtextデータとラベルをBERTを学習する際のデータセット(Dataset形式)に整形します。
5.2.BERTモデルとTokenizerのインポート
from transformers import BertForSequenceClassification, BertTokenizerFast #文章分類用のBertモデルの読み込み id2label = {0: "anger", 1: "joy"} label2id = {"anger": 0, "joy": 1} sc_model = BertForSequenceClassification.from_pretrained('bert-base-uncased', num_labels=2, id2label=id2label, label2id=label2id) #トークナイザを読み込む tokenizer = BertTokenizerFast.from_pretrained("bert-base-uncased") print(sc_model)
transformersライブラリの中にはBERT学習済みモデルや学習済みBERTを使用したファインチューニング用モデルを提供しています。今回はその中でもテキストの分類を行うためのモデルBertForSequenceClassificationを使用します。
BertForSequenceClassification(
(bert): BertModel(
(embeddings): BertEmbeddings(
(word_embeddings): Embedding(30522, 768, padding_idx=0)
(position_embeddings): Embedding(512, 768)
(token_type_embeddings): Embedding(2, 768)
(LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)
(dropout): Dropout(p=0.1, inplace=False)
)
(encoder): BertEncoder(
(layer): ModuleList(
(0-11): 12 x BertLayer(
(attention): BertAttention(
(self): BertSelfAttention(
(query): Linear(in_features=768, out_features=768, bias=True)
(key): Linear(in_features=768, out_features=768, bias=True)
(value): Linear(in_features=768, out_features=768, bias=True)
(dropout): Dropout(p=0.1, inplace=False)
)
(output): BertSelfOutput(
(dense): Linear(in_features=768, out_features=768, bias=True)
(LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)
(dropout): Dropout(p=0.1, inplace=False)
)
)
(intermediate): BertIntermediate(
(dense): Linear(in_features=768, out_features=3072, bias=True)
(intermediate_act_fn): GELUActivation()
)
(output): BertOutput(
(dense): Linear(in_features=3072, out_features=768, bias=True)
(LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)
(dropout): Dropout(p=0.1, inplace=False)
)
)
)
)
(pooler): BertPooler(
(dense): Linear(in_features=768, out_features=768, bias=True)
(activation): Tanh()
)
)
(dropout): Dropout(p=0.1, inplace=False)
(classifier): Linear(in_features=768, out_features=2, bias=True)
)
ネットワークを確認してみると、単語のベクトル化や位置情報の埋め込み等を行うembeddingsレイヤー、その後にtransoformerのエンコーダで12回のMultiHeadSelfAttention処理が行われるencoderレイヤー、最後にencoderレイヤーでの出力を二値分類用に出力を変換するclassifierレイヤーで構成されていることが分かります。

5.3.データの読み込み/準備
import pandas as pd import numpy as np file = './drive/MyDrive/Emotions.xlsx' data = pd.read_excel(file, index_col=0) data = data.T[['anger', 'joy']].T #データ分割 from sklearn.model_selection import train_test_split train_data, eval_data = train_test_split(data, test_size=0.2, random_state=1995, stratify=data.index) train_data['label'] = train_data.index train_data = train_data.reset_index() eval_data['label'] = eval_data.index eval_data = eval_data.reset_index() train_data = train_data.drop(['Field1'], axis=1) eval_data = eval_data.drop(['Field1'], axis=1) #ラベルを数値に変換する from sklearn.preprocessing import LabelEncoder class_le = LabelEncoder() train_data['label'] = class_le.fit_transform(train_data['label']) eval_data['label'] = class_le.fit_transform(eval_data['label'])
データをpandas.DataFrame形式で読み込んでラベルを数値に変換して学習データと評価用データに分割しました。先述したように今回はラベルがangerとjoyのもののみを使用します。
from datasets import Dataset, DatasetDict train_dataset = Dataset.from_pandas(train_data) eval_dataset = Dataset.from_pandas(eval_data) print(train_dateset)
datesetsモジュールのDataset.from_pandasを使用してpandas.DataFrame形式のデータをDataset形式のデータに変換します。
Dataset({
features: ['SIT', 'label'],
num_rows: 1752
})
続いて、tokenizerを使用して、テキスト内の単語を一意の数値に変換します。Dataset形式のデータはmap関数を使用することでバッチで処理を実行できます。
def preprocess_text_classification(example): encoded_example = tokenizer(example['SIT'], max_length=256) encoded_example['labels'] = example['label'] return encoded_example encoded_train_dataset = train_dataset.map(preprocess_text_classification, remove_columns=train_dataset.column_names) encoded_eval_dataset = eval_dataset.map(preprocess_text_classification, remove_columns=eval_dataset.column_names)
tokenizerを通ったデータは以下のように'input_ids', 'token_type_ids', 'attention_mask', 'labels'というカラムを持っています。
encoded_train_dataset
Dataset({
features: ['input_ids', 'token_type_ids', 'attention_mask', 'labels'],
num_rows: 1752
})
実際に0番目のデータを確認してみます。
print(encoded_train_dataset[0])
{'input_ids': [101, 1045, 2018, 2025, 2464, 2026, 2567, 2005, 2274, 2086, 2004, 2002, 2001, 2025, 1999, 3577, 1012, 1037, 2043, 2002, 3369, 2012, 1996, 3199, 1010, 1045, 2371, 2307, 6569, 1012, 102], 'token_type_ids': [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], 'attention_mask': [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], 'labels': 1}
input_idsにはテキスト内の単語が一意の数値に変換されたものが格納されています。token_type_idsには全て0が格納されています。二つのセンテンスのつながりの整合性を予測するようなタスクの場合、同一センテンス内の単語は同一の値になるように設定する必要があります。attention_maskは学習時にマスクをするかどうかを示します。今回は全てに1が入っているのでマスクはしません。
#バッチごとにパディングしてサイズを揃える from transformers import DataCollatorWithPadding data_collator = DataCollatorWithPadding(tokenizer=tokenizer)
最後に数値化したテキストデータが全てのサンプルで同じサイズになるようにするDataCollatorWithPaddingクラスをインスタンス化しておきます。ニューラルネットワークモデルでは入力サイズを統一しておく必要があるので、最大サイズとなるサンプルとサイズが同じになるように足りない分を0で埋める処理を行います。ここでインスタン化したインスタンスは後程BERTモデルをインスタンス化する際に使用します。
5.4.BERTモデルの定義
TrainingArgumentsクラスをインスタンス化する際に学習時のハイパーパラメータ等を設定できます。
#学習に関わる設定 from transformers import TrainingArguments training_args = TrainingArguments( output_dir = './results', logging_dir = './logs', num_train_epochs = 1, per_device_train_batch_size = 8, per_device_eval_batch_size= 32, warmup_steps=500, weight_decay = 0.01, evaluation_strategy='steps' )
5.5.BERTモデルの訓練(ファインチューニング)/精度検証
分類精度の評価用に以下の関数を作成しておきます。
#評価用の関数 from sklearn.metrics import accuracy_score def compute_metrics(result): labels = result.label_ids preds = result.predictions.argmax(-1) acc = accuracy_score(labels, preds) return {'accuracy': acc}
いよいよ学習済みのBERTモデルを使用したファインチューニングを行います。 Trainerクラスを使用することで簡単に学習が行えます。
from transformers import Trainer #Trainerクラスのインスタンス化 trainer = Trainer( model=sc_model, args = training_args, compute_metrics=compute_metrics, train_dataset=encoded_train_dataset, eval_dataset = encoded_eval_dataset, data_collator=data_collator, ) #学習 trainer.train()
以下のようなログが学習中に表示されます。
***** Running training *****
Num examples = 1752
Num Epochs = 1
Instantaneous batch size per device = 8
Total train batch size (w. parallel, distributed & accumulation) = 8
Gradient Accumulation steps = 1
Total optimization steps = 219
Number of trainable parameters = 109483778
You're using a BertTokenizerFast tokenizer. Please note that with a fast tokenizer, using the `__call__` method is faster than using a method to encode the text followed by a call to the `pad` method to get a padded encoding.
[219/219 00:29, Epoch 1/1]
Step Training Loss Validation Loss
Training completed. Do not forget to share your model on huggingface.co/models =)
TrainOutput(global_step=219, training_loss=0.43091018885782323, metrics={'train_runtime': 32.6082, 'train_samples_per_second': 53.729, 'train_steps_per_second': 6.716, 'total_flos': 47150323342560.0, 'train_loss': 0.43091018885782323, 'epoch': 1.0})
学習が行えたので、バリデーションデータに対する精度検証を行います。
trainer.evaluate()
***** Running Evaluation *****
Num examples = 438
Batch size = 32
[14/14 01:37]
{'eval_loss': 0.13717880845069885,
'eval_accuracy': 0.95662100456621,
'eval_runtime': 1.4407,
'eval_samples_per_second': 304.009,
'eval_steps_per_second': 9.717,
'epoch': 1.0}
正解率は95%という結果となりました。
#学習済みモデルの保存 import os !mkdir -p drive/MyDrive/emotion-bert !cp -r results drive/MyDrive/emotion-bert base_path = './drive/MyDrive/emotion-bert/' model_path = base_path + 'model/' if not os.path.exists(model_path): os.mkdir(model_path) sc_model.save_pretrained(model_path) tokenizer.save_pretrained(model_path)
グーグルドライブをマウントしてファインチューニング後のモデルを保存しておきます。
モデルの読み込みは下記で行えます。
#モデル読み込み
loaded_model = BertForSequenceClassification.from_pretrained(model_path)
loaded_tokenizer = BertTokenizerFast.from_pretrained(model_path)
5.6.予測結果の確認
pipelineを使うと、テキストデータを与えると予測ラベルや確信度を返してくれる。 ファインチューニング後のBERTとTokenizerを指定してインスタンス化を行う。
from transformers import pipeline sc_pipeline = pipeline("sentiment-analysis", model=loaded_model, tokenizer=loaded_tokenizer)
例えば、バリデーション用のテキストデータを与えると、
sc_pipeline(eval_dataset['SIT'][1])
以下のように予測ラベルと確信度が返ってきます。
[{'label': 'joy', 'score': 0.9818763136863708}]
それではこのpipelineを使用してバリデーションデータに対する二値分類混合行列を作成してみます。
#resultsに各バリデーションデータに対する予測ラベル、正解ラベル、確信度を格納していきます。 results = [] for i in eval_data.index: model_pred = sc_pipeline(eval_data['SIT'][i])[0] true_label = id2label[eval_data['label'][i]] results.append( { "id" : i, "pred_prob": model_pred['score'], "pred_label" : model_pred['label'], "true_label" : true_label, } )
続いて混合行列を作成します。
import matplotlib.pyplot as plt from sklearn.metrics import ConfusionMatrixDisplay, confusion_matrix #混合行列の作成 confusion_matrix = confusion_matrix( y_true=[result['true_label'] for result in results], y_pred=[result['pred_label'] for result in results], labels=['anger', 'joy'] ) #混合行列を画像として描画 ConfusionMatrixDisplay( confusion_matrix, display_labels=['anger', 'joy'] ).plot()

最後に予測が誤った事例を確認してみます。
#予測が誤った事例を確認する failed_results = [res for res in results if res['pred_label'] != res['true_label']] for result in failed_results: text = eval_data['SIT'][result['id']] print(f"テキスト:{text}") print(f"予測:{result['pred_label']}") print(f"正解:{result['true_label']}") print(f"予測確率:{result['pred_prob']:.4f}") print("-------------------------------------")
以下が予測が誤った事例です。
テキスト:Found money on the road and returned it to the owner through á police. 予測:anger 正解:joy 予測確率:0.9824 ------------------------------------- テキスト:I was stood up for a date function by someone who I really cared á for. 予測:joy 正解:anger 予測確率:0.8022 ------------------------------------- テキスト:[ No description.] 予測:joy 正解:anger 予測確率:0.8959 ------------------------------------- テキスト:In a conversation my boyfriend expressed definite and quite á pretentious opinions and he took up an attitude towards a theory á which he himself had never known. His information was from á fortuitous sources. 予測:joy 正解:anger 予測確率:0.9674 ------------------------------------- テキスト:Two years ago, somebody I like very much wanted to give up his á studies. I tried to make him understand the importance of what he á was going to do, not only of the difficulty to find a job but also á because he will decrease his culture etc. This person 予測:anger 正解:joy 予測確率:0.8549 ------------------------------------- テキスト:Blank. 予測:anger 正解:joy 予測確率:0.8191 ------------------------------------- テキスト:My little niece, who is very talkative, suddenly became very á naughty and began wetting her pants. She did it one afternoon. 予測:joy 正解:anger 予測確率:0.9705 ------------------------------------- テキスト:This week I was phoned by an old friend with whom I lost contact á a few years ago. 予測:anger 正解:joy 予測確率:0.5844 ------------------------------------- テキスト:When I found out that the guy I was dating at a particular time á had a steady relationship going on with someone else for a long á time. 予測:joy 正解:anger 予測確率:0.9733 ------------------------------------- テキスト:The stories about the way my grandmother treated my mother. 予測:joy 正解:anger 予測確率:0.9004 ------------------------------------- テキスト:The sight of a man who ran amok (fighting) at a dance. 予測:joy 正解:anger 予測確率:0.7689 ------------------------------------- テキスト:Discussing psychology with my friends before the lecture. 予測:anger 正解:joy 予測確率:0.7103 ------------------------------------- テキスト:A month ago when one of my fellow workers got a promotion over á me. It was just a small promotion but recognition was involved. 予測:joy 正解:anger 予測確率:0.9798 ------------------------------------- テキスト:I got my driving licence after they had frightened me with it's á difficulty. 予測:anger 正解:joy 予測確率:0.9134 ------------------------------------- テキスト:A member of a religious sect tried to convert me, using really á evil tricks to persuade me. After he had left, I was anxious and á angry for a long time. After the event, I was alone. 予測:joy 正解:anger 予測確率:0.7611 ------------------------------------- テキスト:Being asked to go out by someone I care. 予測:anger 正解:joy 予測確率:0.9723 ------------------------------------- テキスト:When my mother kept me in leading-strings. 予測:joy 正解:anger 予測確率:0.9706 ------------------------------------- テキスト:A father helping his kid to fight other kids. 予測:joy 正解:anger 予測確率:0.9776 -------------------------------------
ここで一つピックアップしてみてみます。
テキスト:This week I was phoned by an old friend with whom I lost contact á a few years ago. 予測:anger 正解:joy 予測確率:0.5844
この事例では、「連絡をとっていなかった旧友人から電話がかかってきた」というハッピーなニュースですが、モデルは'anger'と予測してしまっています。ただ、確信度は低く、やや判定に迷っていることが伺えます。
この分の中に’lost'というネガティブなワードが入っているのでこのワードを除くと予測はどうなるか見てみます。
sc_pipeline("This week I was phoned by an old friend with whom I contact á a few years ago.")
結果は'joy'となりました!
[{'label': 'joy', 'score': 0.9774478673934937}]
'lost'というワードによって誤った予測になってしまっていたことが分かりました。文脈を学習するBERTですが、ある1単語が予測に大きな影響を与えることもあるようです。
6.参考文献
混合モデルによる潜在変数の特定(PyMC3)


1.背景
観測データの背後にある構造を把握することで有用な示唆を得られることがある。今回は簡単のために以下のような時系列データを考えてみる。下記はある人の心拍数の時間変位を想定して生成したデータである。今回、心拍数を決定づけるモードに平時、軽運動時、重運動時を想定し、観測されるデータから測定者が特定のタイミングでどのようなモードにあったのかを特定したい。混合モデルを使用することでモードの特定が可能になる。

2.混合モデル(Mixture Model)
混合モデル(Mixture Model)は、統計モデリングの手法の一つで、複数の確率分布の組み合わせでデータをモデル化する方法である。混合モデルは、複数の異なるデータ生成プロセスが同じデータセット内で共存している場合に適している。各データポイントは、異なる確率分布のいずれかから生成されたものと仮定される。
具体的な例を挙げると、ガウス混合モデル(Gaussian Mixture Model, GMM)がよく知られる。GMMは、複数のガウス分布(正規分布)を組み合わせてデータをモデル化する。各ガウス分布は、異なる部分集合のデータを表現し、それぞれが異なる平均値と分散を持つ。データポイントは、これらのガウス分布のどれかからランダムに選ばれると仮定される。
混合モデルは一般的に以下の要素により構成される。
成分(Component): 各確率分布を成分と呼び、混合モデルではこれらの成分が複数存在する。各成分は異なる特性やパラメータ(平均、分散など)を持つ。
混合比率(Mixture Weights): 各成分がデータセットにどの程度の割合で存在するかを表すパラメータ。これらの混合比率は、各成分がデータに対して寄与する程度を調整する。
確率密度関数(Probability Density Function, PDF): 各成分に関連する確率密度関数が定義される。これは、ある成分が与えられたデータポイントを生成する確率を示す。
混合モデルは、クラスタリング、異常検知、特徴の抽出などのさまざまな応用分野で利用される。GMM以外にも、ポアソン混合モデルや指数混合モデルなど、様々な種類の混合モデルが存在する。データの複雑な構造をモデル化する際に有用な手法である。
3.PyMC3によるポアソン混合モデルの実装
人の心拍数の時間変位疑似データを生成し、PyMC3を使用した混合ポアソンモデルにより、特定のタイミングでどのような運動モードであったか特定してみる。
3.1.データの生成
下記のように疑似データを生成する。以下のコードでは、平時をλ=60、軽運動時をλ=90、重運動時をλ=110のポアソン分布にそれぞれ従うとし、状態遷移行列を定義し、各状態から別の状態へ状態遷移行列に基づいて遷移させ、その状態でのポアソン分布からのサンプリングによりデータを生成する。
import numpy as np import pymc3 as pm import theano.tensor as tt import matplotlib.pyplot as plt import seaborn as sns sns.set() # データ生成 np.random.seed(42) n_states = 3 n_observation = 200 # 遷移確率行列 transition_probs = np.array([[0.9, 0.05, 0.05], [0.05,0.9, 0.05], [0.05, 0.05, 0.9]]) # 隠れ状態の初期確率 initial_probs = np.array([1.0, 0.0, 0.0]) # 隠れ状態の生成 hidden_states = [np.random.choice(range(n_states), p=initial_probs)] for _ in range(n_observation - 1): hidden_states.append(np.random.choice(range(n_states), p=transition_probs[hidden_states[-1]])) # 観測モデルのパラメータ obs_means = np.array([60, 90 ,110]) # ポアソン分布の平均パラメータ # 観測データの生成 observed_data = np.random.poisson(obs_means[hidden_states])
以下が生成したデータと各時刻での運動モード(0:平時、1:弱運動、2:重運動)である。ベイズモデリングによる混合ポアソンモデルを用いることでこの特定の時刻の運動モードを推定する。


3.2.混合ポアソンモデルの実装
ベイズモデリングにより混合ポアソンモデルを実装する。特定の時刻の心拍数は3つの運動モードのうち、どれか1つの運動モードに属するとし、各モードはパラメータλに基づくポアソン分布に従うとしてモデル化する。また、それぞれのモードのポアソン分布のパラメータλの事前分布には一様分布、カテゴリカル分布の事前分布にはディレクレ分布を設定する。
K = 3 with pm.Model() as model: #混合比率 pi = pm.Dirichlet("pi", a=10*np.ones(K), shape=K) #クラスタ毎のポアソン分布のパラメータ mu = pm.Uniform("mu", lower=0, upper=60, shape=K) z = pm.Categorical("z", p=pi, shape=n_observation) x = pm.Poisson('obs', mu=mu[z], observed=observed_data)

モデル化ができたので、MCMC法を用いて事後分布のサンプリングをする。
with model: trace = pm.sample(2000, tune=1000, chains=4, random_seed=42)
サンプリング結果を可視化する。
_ = pm.traceplot(trace) _ = pm.plot_posterior(trace)
traceplotではサンプリングの分布が確認できる。
 plot_posteriorでは特定の時刻で各モードに属する確率が可視化できる。
plot_posteriorでは特定の時刻で各モードに属する確率が可視化できる。

サマリーを確認する。
pm.summary(trace)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
z[0] 0.000 0.016 0.000 0.000 0.000 0.000 8016.0 8016.0 1.0
z[1] 1.946 0.226 2.000 2.000 0.005 0.003 2378.0 2378.0 1.0
z[2] 2.000 0.016 2.000 2.000 0.000 0.000 8018.0 8000.0 1.0
z[3] 1.804 0.397 1.000 2.000 0.007 0.005 3655.0 3655.0 1.0
z[4] 2.000 0.011 2.000 2.000 0.000 0.000 8016.0 8000.0 1.0
... ... ... ... ... ... ... ... ... ...
pi[1] 0.369 0.034 0.302 0.431 0.000 0.000 4880.0 6001.0 1.0
pi[2] 0.276 0.032 0.218 0.336 0.000 0.000 6841.0 6050.0 1.0
mu[0] 58.796 0.959 56.966 60.578 0.011 0.008 7621.0 5323.0 1.0
mu[1] 98.230 1.404 95.687 100.914 0.023 0.016 3870.0 5212.0 1.0
mu[2] 137.769 1.887 134.301 141.397 0.031 0.022 3821.0 5276.0 1.0
最後に今回モデル化した混合ポアソンモデルによって推定される運動モードと実際の運動モードを比較してみる。 traceに観測データを持ちいて更新された事後データが格納されている。trace['z']に特定の時刻での各モードに属する確率が格納されているのでその中で最大となるindex(モード)を推定値とする。以下のコードにより特定の時刻でのモードの推定値を抽出できる。
mode_ = [] for i in range(0, n_observation): unique, freq = np.unique(trace['z'][:, i], return_counts=True) mode = unique[np.argmax(freq)] mode_.append(mode)
以下が実際の運動モード(左図)と推定した運動モード(右図)の比較である。隣接するモード間ではところどころ推定ミスはあるもののモードをよく推定できている。


生存時間解析をやってみる2(PyMC3)


masao-ds.hatenablog.com ベイズモデリングによる生存時間解析はこちらを参考にしてください。
1.やりたいこと/課題設定
ある工場ではとある製品を量産している。複数台の生産装置を使用して製品を量産しているが、装置の故障が多発し、製品を生産することができず機会損失が生じていた。そこで生産装置を別の故障時間が長いものに入れ替えることにした。ベイズモデリングによる生存時間により、入れ替え前と後の生産装置での1ヶ月稼働時(装置メンテナンスを1ヶ月と想定)の機会損失額の差を見積もりたい。
2.ベイズモデリングによる生存時間解析を用いた機会損失額の比較
2つの故障時間が異なる生産装置の故障時間データを作成し、ベイズモデリングによる生存時間解析を行い、故障時間をモデル化する。その後、1ヶ月間工場で納入している生産装置で生産を行う場合の機会損失額を2つの異なる生産装置で比較する。この際、工場への生産装置の納入数は50台、1日1台あたりの生産個数は100個、製品1個あたりの売上は100円とする。
2.1.データの生成
まず故障時間の異なる架空の故障データを作成する。
#旧装置 # ワイブル分布のパラメータ shape_old = 2 # ワイブル分布の形状パラメータ scale_old = 28.0 # ワイブル分布の尺度パラメータ # ランダムな故障時間を生成 np.random.seed(42) # 乱数のシードを設定(再現性のため) failures_old = np.random.weibull(shape_old, size=100) * scale_old #新装置 # ワイブル分布のパラメータ shape_new = 3.0 # ワイブル分布の形状パラメータ scale_new = 35.0 # ワイブル分布の尺度パラメータ # ランダムな故障時間を生成 np.random.seed(42) # 乱数のシードを設定(再現性のため) failures_new = np.random.weibull(shape_new, size=100) * scale_new
plt.hist(failures_old, alpha=0.5) plt.hist(failures_new, alpha=0.5) plt.show()

変更後の生産装置の方が故障までの時間が長くなるように生成した。また、以下のように40日経過後のデータは打切りデータとして扱うことにした。
#40日よりも後を身観測データとする。 df_failures_old=pd.DataFrame(failures_old, columns=['Time']) df_failures_old['censored'] = df_failures_old['Time'] >= 40 y_old = df_failures_old['Time'].values censored_old = df_failures_old['censored'].values df_failures_new=pd.DataFrame(failures_new, columns=['Time']) df_failures_new['censored'] = df_failures_new['Time'] >= 40 y_new = df_failures_new['Time'].values censored_new = df_failures_new['censored'].values
2.2.装置の生存時間解析
2.2.1.変更前の装置の生存時間解析
PyMC3を使用したベイズモデリングを行う。生存時間分布にはワイブル分布を仮定する。
def weibull_lccdf(x, alpha, beta): """ Log complementary cdf of Weibull distribution. """ return -((x / beta) ** alpha) #打ち切りなしデータ+打ち切りありデータ with pm.Model() as model_2: alpha_sd = 10.0 mu = pm.Normal("mu", mu=0, sigma=100) alpha_raw = pm.Normal("a0", mu=0, sigma=0.1) alpha = pm.Deterministic("alpha", tt.exp(alpha_sd * alpha_raw)) beta = pm.Deterministic("beta", tt.exp(mu / alpha)) y_obs = pm.Weibull("y_obs", alpha=alpha, beta=beta, observed=y_old[~censored_old]) #事後対数尤度に制約としてつけ加える。この項を含めた事後対数尤度が最大になるようにMCMCでサンプリングする。 y_cens = pm.Potential('y_cens', weibull_lccdf(y_old[censored_old], alpha, beta)) with model_2: trace_2 = pm.sample(target_accept=0.9, init="adapt_diag")
事後サンプリング結果をプロットする。
_ = pm.traceplot(trace_2) _ = pm.plot_posterior(trace_2)

サマリーを確認。
pm.summary(trace_2)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
mu 5.626 0.497 4.644 6.535 0.020 0.014 637.0 651.0 1.01
a0 0.052 0.008 0.036 0.068 0.000 0.000 668.0 642.0 1.01
alpha 1.692 0.140 1.439 1.974 0.005 0.004 668.0 642.0 1.01
beta 27.813 1.812 24.422 31.111 0.034 0.024 2768.0 2268.0 1.00
2.2.2.変更後の装置の生存時間解析
同様にPyMC3を使用したベイズモデリングにより生存時間解析を行う。
with pm.Model() as model_3: alpha_sd = 10.0 mu = pm.Normal("mu", mu=0, sigma=100) alpha_raw = pm.Normal("a0", mu=0, sigma=0.1) alpha = pm.Deterministic("alpha", tt.exp(alpha_sd * alpha_raw)) beta = pm.Deterministic("beta", tt.exp(mu / alpha)) y_obs = pm.Weibull("y_obs", alpha=alpha, beta=beta, observed=y_new[~censored_new]) #事後対数尤度に制約としてつけ加える。この項を含めた事後対数尤度が最大になるようにMCMCでサンプリングする。 y_cens = pm.Potential('y_cens', weibull_lccdf(y_new[censored_new], alpha, beta)) with model_3: trace_3 = pm.sample(target_accept=0.9, init="adapt_diag")
事後サンプリング結果をプロットする。
_ = pm.traceplot(trace_3) _ = pm.plot_posterior(trace_3)
サマリーを確認する。
pm.summary(trace_3)
sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat mu 8.309 0.755 6.915 9.784 0.031 0.022 591.0 635.0 1.01 a0 0.084 0.009 0.067 0.101 0.000 0.000 585.0 615.0 1.01 alpha 2.319 0.206 1.898 2.693 0.009 0.006 585.0 615.0 1.01 beta 36.039 1.737 32.854 39.437 0.032 0.023 2977.0 2575.0 1.00
2.3.故障時間の比較
以下のようなワイブル分布において、特定の時刻までに生存している確率を算出する関数を定義する。
# cdf def weibCumDist(x, a, b): return np.exp(-(x / b) ** a)
続いて、故障時間の分布をプロットする。ベイズモデリングではワイブル分布のパラメータを確率的に決定するため、生存時間分布も幅を持った推定が可能になる。
#サンプル数 n_sim = 2000 t = np.linspace(0, 90 , 90) weibCum_2 = np.zeros((t.shape[0], n_sim)) weibCum_3 = np.zeros((t.shape[0], n_sim)) np.random.seed(42) rand_val = pd.Series(np.random.randint(1000, 4000, n_sim)) k = 0 for val in rand_val: weibCum_2[:, k] = weibCumDist(t, trace_2['alpha'][val], trace_2['beta'][val]) weibCum_3[:, k] = weibCumDist(t, trace_3['alpha'][val], trace_3['beta'][val]) k+=1 plt.plot(t, weibCum_2.mean(axis=1)) plt.fill_between(t, np.percentile(weibCum_2, 95, axis=1), np.percentile(weibCum_2, 5, axis=1), alpha=0.5, label='old') plt.plot(t, weibCum_3.mean(axis=1)) plt.fill_between(t, np.percentile(weibCum_3, 95, axis=1), np.percentile(weibCum_3, 5, axis=1), alpha=0.5, label='new') plt.legend() plt.xlabel('Time[Day]') plt.ylabel('Probability') plt.show()

2.4.損失額の比較
最後に機会損失額の分布を比較する。
def predict_loss_sample(trace, rand_v, time_to): alpha_sim = trace['alpha'][rand_v] beta_sim = trace['beta'][rand_v] t_sim = pd.Series(np.linspace(0, int(time_to), int(time_to) + 1)) F_t = weibCumDist(t_sim, alpha_sim, beta_sim) return F_t.values * 1000 * 100 #生存確率*生産個数*1個あたり売り上げ n_sim = 50 loss_2 = np.zeros(n_sim) loss_3 = np.zeros(n_sim) np.random.seed(42) rand_val = pd.Series(np.random.randint(0, 2000, n_sim)) k = 0 for val in rand_val: loss_2[k] = sum(predict_loss_sample(trace_2, val, 30)) loss_3[k] = sum(predict_loss_sample(trace_3, val, 30)) k += 1 plt.hist(loss_2, alpha=0.5, label='old') plt.hist(loss_3, alpha=0.5, label='new') plt.legend() plt.xlabel('Opportunity loss amount') plt.ylabel('Density') plt.show()
以下、機械損失額の分布の比較。

機会損失額の差の分布を見てみる。
 生産装置を入れ替えることで2万円〜7万円の機会損失を抑制できることがわかる。ベイズモデリングによる生存時間解析では,このように確率的に生存時間を推定できるため、機会損失額を分布で予測することが可能である。
生産装置を入れ替えることで2万円〜7万円の機会損失を抑制できることがわかる。ベイズモデリングによる生存時間解析では,このように確率的に生存時間を推定できるため、機会損失額を分布で予測することが可能である。
生存時間解析をやってみる1(PyMC3)


1.生存時間解析
生存時間解析は、医療分野や工学分野を始めとした様々な領域で重要な統統計的手法として広く利用されています。この手法は、時間の経過とともに特定のイベントが発生するまでの時間を推定し、その確率や影響要因を明らかにするための有力な方法です。生存時間解析は、通常、イベントが発生するまでの時間、あるいは生存期間と呼ばれる期間に注目します。例えば、がん患者の場合、治療開始から再発や死亡が起こるまでの期間や製品の故障発生までの期間が生存期間に相当します。来の統計手法では、時間の要素を考慮することが難しいため、生存時間解析が開発されました。この手法では、生存関数とハザード関数という特別な統計的ツールを用いて、生存期間の分布や特定の時点でのイベント発生の危険性を推定することが可能です。生存時間解析の利点は、データの欠損を扱う能力や、イベントが発生しないまま終了する(censored)データを考慮することができる点にあります。これによりイベント発生をまたず、イベントがその時刻まで発生しなかったという情報をモデルに盛り込み、より妥当な生存時間を推定できます。
生存時間解析には指数分布やワイブル分布が用いられます。指数分布を用いる場合は、ハザード(特定の時点でのイベント発生確率)は一定になります。ハザードを時間に依存して変化させたモデル化を行いたい場合、ワイブル分布を用います。$a,b$を正の数とすると、密度分布は以下で表せます($x\geq 0$)。
ワイブル分布は発生確率に時間依存性を許容した一般化に対応するため、故障現象を説明するためによく用いられます。発生確率は以下の式で表され、$b=1$の場合に時間に対する依存性がなくなり指数分布に合致します。
ここで、$b$は発生確率の時間依存性の指数部分を決める項で、1より大きければ単調増加、小さければ単調減少となり、それぞれ摩耗的な故障、初期的な故障と対応付けることが可能です。
2.PyMC3による生存時間解析の実装
生存時間解析(故障時間解析)を行う場合、以下のようなデータを使用して解析を行っていくことになる。生存時間解析では、途中で打ち切られるデータ(少なくともその時間までは生存していた時間)も重要な情報となる。たとえば、架空の装置の故障データを使用して装置寿故障に関する生存時間解析を考える場合、Timeカラムは故障発生が発生する時間に相当する。Censoredカラムは観測の打ち切りを表す。Falseの場合、観測は打ち切られず装置がTimeカラムの時間で故障したことを表す。Trueの場合は、観測が打ち切られたことを示し、Timeカラムに記載の時間はその時間までは装置は故障せずに稼働していたことを示す。
| No | Time | Censored |
|---|---|---|
| sample_1 | 27 | False |
| sample_2 | 50 | True |
| sample_3 | 10 | False |
| sample_4 | 40 | True |
| sample_5 | 33 | False |
それでは架空の装置に関する生存時間解析(故障時間解析)をPyMC3で行ってみる。 ワイブル分布を用いてモデリングしてみる。 今回打切りなしデータ(実施の故障観測データ)のみでモデル化する場合と打切りなしデータ、打切りありデータ両方を使用してモデル化した場合の結果を比較してみたいと思う。
2.1.データの作成
ワイブル分布を仮定して架空の装置の故障データを生成します。
import numpy as np import pandas as pd import arviz as az import pymc3 as pm from theano import shared, tensor as tt import seaborn as sns import matplotlib.pyplot as plt sns.set() # ワイブル分布のパラメータ shape = 2 # ワイブル分布の形状パラメータ scale = 28.0 # ワイブル分布の尺度パラメータ # ランダムな故障時間を生成 np.random.seed(42) # 乱数のシードを設定(再現性のため) failures = np.random.weibull(shape, size=100) * scale plt.hist(failures) plt.xlabel('Time[Day]') plt.ylabel('Count') plt.show()

データ生成後、40日以降のデータは故障発生時刻ではなく、観測打切りデータとして扱って生存時間解析を進めてみます。
#40日よりも後を観測打切りデータとする。 df_failures=pd.DataFrame(failures, columns=['Time']) #打ち切りかどうかを示すCensoredラムを追加する。 df_failures['censored'] = df_failures['Time'] >= 40 y = df_failures['Time'].values censored = df_failures['censored'].values df_failures.head()
Time censored 0 19.180881 False 1 48.579164 True 2 32.129871 False 3 26.753448 False 4 11.531951 False
2.2.打ち切りなしデータのみを用いた生存時間解析
#打ち切りなしデータのみでベイズ推論 with pm.Model() as model_1: alpha_sd = 10.0 #ワイブル分布の形状パラメータのパラメータの事前分布 mu = pm.Normal("mu", mu=0, sigma=100) #ワイブル分布の形状パラメータのパラメータの事前分布 alpha_raw = pm.Normal("a0", mu=0, sigma=0.1) #ワイブル分布の形状パラメータ alpha = pm.Deterministic("alpha", tt.exp(alpha_sd * alpha_raw)) #ワイブル分布の尺度パラメータ beta = pm.Deterministic("beta", tt.exp(mu / alpha)) #ワイブル分布からのサンプリング y_obs = pm.Weibull("y_obs", alpha=alpha, beta=beta, observed=y[~censored]) #MCMCによるサンプリング with model_1: trace_1 = pm.sample(target_accept=0.9, init="adapt_diag")
サマリーの確認
pm.summary(trace_1)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat mu 6.946 0.612 5.849 8.083 0.024 0.017 678.0 901.0 1.01 a0 0.079 0.008 0.063 0.094 0.000 0.000 711.0 926.0 1.01 alpha 2.209 0.182 1.885 2.550 0.007 0.005 711.0 926.0 1.01 beta 23.197 1.184 20.902 25.344 0.025 0.017 2300.0 2355.0 1.00
サンプリング結果をプロット
_ = pm.traceplot(trace_1) _ = pm.plot_posterior(trace_1)

ベイズモデリングで推定したパラメータを使用してワイブル分布の各時刻の故障確率(pdf)と特定の時刻までの生存確率(cdf)を算出する関数を準備しておく。 なお、cfdはその時刻までの各時刻での故障発生確率(pdf)を時間で積分することで得られる。
# pdf def weibProbDist(x, a, b): return (a / b) * (x / b) ** (a - 1) * np.exp(-(x / b) ** a) # cdf def weibCumDist(x, a, b): return np.exp(-(x / b) ** a)
ベイズモデリングにより推定したパラメータを使用して各時刻の故障発生確率(左)と各時刻までの故障発生確率(右)を可視化する。
shape_ = 2.209 scale_ = 23.197 t = np.linspace(1, 90 ,90) plt.plot(t, weibProbDist(t, shape_, scale_)) plt.title('pdf') plt.xlabel('Time[Day]') plt.ylabel('Probability') plt.show() plt.plot(t, weibDumDist(t, shape_, scale_)) plt.title('pdf') plt.xlabel('Time[Day]') plt.ylabel('Probability') plt.show()


打切りなしデータのみでモデルを作成しているためcdfをみると40日以降の生存確率はほぼ0になっており、本来は40日以降にも故障せずに稼働している装置が存在することを考慮できていない。
2.3.打ち切りなし+打ち切りありデータを用いた生存時間解析
続いて、打切りデータも取り入れてモデル化してみる。
def weibull_lccdf(x, alpha, beta): """ Log complementary cdf of Weibull distribution. """ return -((x / beta) ** alpha) #打ち切りなしデータ+打ち切りありデータ with pm.Model() as model_2: alpha_sd = 10.0 mu = pm.Normal("mu", mu=0, sigma=100) alpha_raw = pm.Normal("a0", mu=0, sigma=0.1) alpha = pm.Deterministic("alpha", tt.exp(alpha_sd * alpha_raw)) beta = pm.Deterministic("beta", tt.exp(mu / alpha)) y_obs = pm.Weibull("y_obs", alpha=alpha, beta=beta, observed=y[~censored]) #事後対数尤度に制約としてつけ加える。 #この項を含めた事後対数尤度が最大になるようにMCMCでサンプリングする。 y_cens = pm.Potential('y_cens', weibull_lccdf(y[censored], alpha, beta)) with model_2: trace_2 = pm.sample(target_accept=0.9, init="adapt_diag")
上記のように打切りデータをモデルにベイズモデリングの中に組み込めるようにワイブル分布の対数補完累積分布関数を定義している。この関数は与えられたワイブル分布パラメータのもとでx以下になる累積確率の対数値を返す。この値をMCMCの事後対数尤度に加えたものが最大になるようにパラメータを決定する。こうすることで打切りデータが持つ「最低限その時点までは生存していた」という情報を確率としてモデルに組み込むことができる。
サンプリング結果を可視化
_ = pm.traceplot(trace_2) _ = pm.plot_posterior(trace_2)

サマリーの確認
pm.summary(trace_2)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat mu 5.625 0.513 4.622 6.559 0.019 0.014 745.0 628.0 1.0 a0 0.052 0.009 0.037 0.069 0.000 0.000 748.0 622.0 1.0 alpha 1.691 0.145 1.419 1.968 0.005 0.004 748.0 622.0 1.0 beta 27.893 1.840 24.534 31.411 0.034 0.024 2883.0 2072.0 1.0
ベイズモデリングにより推定したパラメータを使用して各時刻の故障発生確率(左)と各時刻までの故障発生確率(右)を可視化する。
shape_2 = 1.691 scale_2 = 27.893 plt.plot(t, weibProbDist(t, shape_2, scale_2)) plt.ylim(0, 0.04) plt.title('pdf') plt.xlabel('Time[Day]') plt.ylabel('Probability') plt.show() plt.plot(t, weibCumDist(t, shape_2, scale_2)) plt.title('cdf') plt.xlabel('Time[Day]') plt.ylabel('Probability') plt.show()


続いて、打切りデータのみの場合と打切りデータと打切りありデータでモデル化した場合の比較をしてみる。


打切りデータを考慮してモデリングが行えているため、40日以降の生存確率が打切りなしデータのみでモデリングした場合よりも高くなっている。生存時間解析では、打切りデータもモデル化に組み込むことができるため、より妥当な生存時間の推定が可能になる。故障発生期間が長い場合,、故障発生データを取得していくには長期間を要する。故障発生を待たず打切りデータとして生存情報を考慮できるのは生存時間解析のメリットである。
PytorchでPINNs(Physics Informed Neural Network)を実装してみる(Burgers方程式)
1.やりたいこと
Burgers方程式に対して、PINNs(Physics Informed Neural Network)を構築し、解析解とPINNsの予測結果を比較してみます。
PINNsに関しては過去のこちらの記事を参考にしてください。
2.Burgers方程式
Burgers方程式は、非線形偏微分方程式の一つであり、流体力学や波動現象のモデリングに使用されます。Burgers方程式は次のように表されます。
一次元のNavier-Stokes方程式から圧力項を除いた式になっています。流体の粘性によって波が拡散し減衰していく様子を解くことができます。
3.問題設定
sin波を初期値に設定した時のBurgers方程式に基づく時間発展をPINNsを使用して予測し、有限差分法による計算結果と比較をしてみます。
4.PINNsによる解法
まず計算領域と時間発展領域を定義し、初期条件(Sin波)と境界条件(計算量領域の両端でu=0)を定義し、データを作成します。
その後、Burges方程式を満たすべき、計算領域及び時間発展領域点をいくらかサンプリングをしたデータを作成します。このサンプリングデータをを与えた時にNNモデルがBurgers方程式を満たすように(最小化するように)学習を行いつつ、初期条件や境界条件での値に対する損失を最小化するような学習モデルを定義します。
4.1.初期条件及び境界条件のデータ作成
計算領域を[-1, 1]で定義し、時間発展領域を[0, 1]sと定義します。t=0[s]での空間位置を初期のデータが存在する点としていくらか作成します(初期条件)。また、任意の時刻の境界上下端(x=-1, 1)のデータをいくらか作成します。初期に解が与えられる空間位置及び空間上下限の時刻はscipy.stats.qmcクラスを使用してランダムにサンプリングして決定します。
import torch import torch.nn as nn import numpy as np import matplotlib.pyplot as plt import seaborn as sns sns.set() from scipy.stats import qmc import scipy #データの作成 #初期条件データ数 n_ic_points = 100 #上側境界条件データ数 n_bc1_points = 50 #下側境界条件データ数 n_bc2_points = 50 #scipy.stats.qmcクラスをインスタンス化(空間データと時間発展の初期及び境界データを生成するのに使用する。) engine = qmc.LatinHypercube(d=1) # 1[s]までの時間を乱数で生成 # 後から境界の下限と上限に割り振る。 t_d = engine.random(n=n_bc1_points + n_bc2_points) # 初期条件なので時刻は0 temp = np.zeros([n_ic_points, 1]) # 初期条件と境界の時間を結合する。 t_d = np.append(temp, t_d, axis=0) # 空間データ # 初期の空間座標 x_d = engine.random(n=n_ic_points) x_d = 2 * (x_d - 0.5) # 境界の空間座標 temp1 = -1 * np.ones([n_bc1_points, 1]) # for BC1 ; x = -1 temp2 = +1 * np.ones([n_bc2_points, 1]) # for BC2 ; x = +1 # 初期条件と境界の座標を結合する。 x_d = np.append(x_d, temp1, axis=0) x_d = np.append(x_d, temp2, axis=0) # データポイントの可視化 plt.figure(figsize=(8, 3)) plt.scatter(t_d, x_d, marker="x", c="k") plt.xlabel("t") plt.ylabel("x") plt.title("Data points (BCs & IC)")
下記が、初期にデータが与えられる空間ポイントと境界のサンプリングです。

続いて、上で作成した初期および境界の空間及び時間データに対して、uの値(教師データ)を与えます。初期条件に対しては、Sin波を与え、境界条件としては任意の時間の境界上下端に対してu=0を与えます。
# 初期条件、境界条件を設定する。 # 初期条件と境界条件で設定した空間ポイントだけ用意する。 y_d = np.zeros(x_d.shape) # 0からn_ic_pointsは初期条件の領域 y_d[ : n_ic_points] = -np.sin(np.pi * x_d[:n_ic_points]) # 境界条件の設定 y_d[n_ic_points : n_bc1_points + n_ic_points] = 0 y_d[n_bc1_points + n_ic_points : n_bc1_points + n_ic_points + n_bc2_points] = 0
4.2.計算領域内のサンプリングデータの作成
Burgers方程式を満たしてほしい空間及び時間発展領域の点を指定した数だけランダムにサンプリングします。後に定義するPINNsモデルの中でここで定義したサンプリングデータを与えたときにBuegers方程式を満たすようにNNの学習を行います。こちらもscipy.stats.qmcクラスを使用してランダムなサンプリングを行います。
# 支配方程式を満たすべき時空間ポイント Nc = 10000 # LHS for collocation points engine = qmc.LatinHypercube(d=2) data = engine.random(n=Nc) # set x values between -1. and +1. data[:, 1] = 2*(data[:, 1]-0.5) # change names t_c = np.expand_dims(data[:, 0], axis=1) x_c = np.expand_dims(data[:, 1], axis=1) t_c = np.vstack([t_c, t_d]) x_c = np.vstack([x_c, x_d]) # データポイントの可視化 plt.figure(figsize=(8, 3)) plt.scatter(t_c, x_c, marker="x", c="k") plt.xlabel("t") plt.ylabel("x") plt.title("Data points (BCs & IC)")
サンプリング点(Burgers方程式を満たしてほしい点)が時空間領域全体で満遍なく生成できていそうです。

4.3.学習モデル定義
PINNs学習用モデルを定義します。まず、NNクラスを定義します。NNクラス内では空間位置と時間を入力すると、その空間位置と時間に対応するuの値を返すニューラルネットワークを定義しています。活性化関数にTanhを使用し、非線形変換を何層か繰り返す多層NNを作成します。このNNクラスをPINNsクラス内でインスタンス化し、NNの重みを初期や境界の教師ペアの最小化を行いつつ、サンプリングしたデータがBurgers方程式を満たすように更新(学習)して行きます。以下がNNクラスの定義コードです。
# モデル、ネットワーク定義 class NN(nn.Module): def __init__(self, n_input, n_output, neuron_per_layer=50): super(NN, self).__init__() #set activation function self.activation = nn.Tanh() self.n_input = n_input self.n_output = n_output self.affine1 = nn.Linear(self.n_input, neuron_per_layer) self.affine2 = nn.Linear(neuron_per_layer, neuron_per_layer) self.affine3 = nn.Linear(neuron_per_layer, neuron_per_layer) self.affine4 = nn.Linear(neuron_per_layer, neuron_per_layer) self.affine5 = nn.Linear(neuron_per_layer, neuron_per_layer) self.affine6 = nn.Linear(neuron_per_layer, neuron_per_layer) self.affine7 = nn.Linear(neuron_per_layer, neuron_per_layer) self.affine8 = nn.Linear(neuron_per_layer, self.n_output) def forward(self, t): t = self.activation(self.affine1(t)) t = self.activation(self.affine2(t)) t = self.activation(self.affine3(t)) t = self.activation(self.affine4(t)) t = self.activation(self.affine5(t)) t = self.activation(self.affine6(t)) t = self.activation(self.affine7(t)) t = self.affine8(t) return t
続いて、PINNsクラスを定義します。
PINNsクラスは. t, x, u :教師がある学習に使用する初期のサンプリングデータ及び境界のサンプリングデータとそれぞれt,xに対応する教師u、x_region, t_region:Burgers方程式を満たしてほしい時空間サンプリングデータのペア及びBurgers方程式のパラメータνを与えることでインスタンス化できる。
PINNsクラスは以下のメソッドを持ちます。
net_uメソッド: 入力として受け取ったx, tのデータをconcatして一次元配列に変換し、インスタンス化されているNNクラスに入力として与え、出力(その学習時点でのuの予測値)を返します。
net_fメソッド: x, tを入力し、自動微分により勾配の計算を行い、学習時点での支配方程式への当てはまり度合いを返します。
loss_funcメソッド: 初期や境界条件の教師があるデータに対する損失と支配方程式への当てはまりを足し合わせて学習時の損失を定義します。
trainメソッド: 学習を行います。
predictメソッド: 定義域内の時空間データのペアを与えることで、学習済モデルを使用してその時空間データに対応するuの予測値を返します。
# PINNsモデルの定義 class PINNs(): def __init__(self, t, t_region, x, x_region, u, nu): self.nu = nu #入力変数を定義 #t, x : 学習に使用する初期条件及び境界条件 #t_region, x_region:支配方程式を満たしているかどうかを評価するために使用する教師なしデータ #u : 学習に使用する初期条件及び境界の教師データ self.t = torch.tensor(t, requires_grad=True).float() self.t_region = torch.tensor(t_region, requires_grad=True).float() self.x = torch.tensor(x, requires_grad=True).float() self.x_region = torch.tensor(x_region, requires_grad=True).float() self.u = torch.tensor(u, requires_grad=True).float() #NNをインスタンス化 self.dnn = NN(2, 1) #optimizers self.optimizer = torch.optim.Adam(self.dnn.parameters(), lr=1e-3) #dnnの入力にできるように空間座標と時間を結合する。 def net_u(self, x, t): u = self.dnn(torch.cat([x, t], dim=1)) return u #現状のエポックスでの支配方程式への当てはまりを計算 def net_f(self, x, t): #現状のエポックスでの予測値 u = self.net_u(x, t) #時間1階微分 u_t = torch.autograd.grad(u, t, grad_outputs=torch.ones_like(u),retain_graph=True, create_graph=True)[0] #空間1階微分 u_x = torch.autograd.grad(u, x, grad_outputs=torch.ones_like(u),retain_graph=True, create_graph=True)[0] #空間2回微分 u_xx = torch.autograd.grad(u_x, x, grad_outputs=torch.ones_like(u_x),retain_graph=True, create_graph=True)[0] f = u_t + u * u_x - self.nu * u_xx return f #損失の評価 def loss_func(self): u_pred = self.net_u(self.x, self.t) f_pred = self.net_f(self.x_region, self.t_region) loss_u = torch.mean((self.u - u_pred)**2) loss_f = torch.mean(f_pred**2) loss = loss_u + loss_f*5e-4 return loss, loss_u, loss_f # 学習 def train(self): epochs = 20000 for epoch in range(epochs): self.dnn.train() self.loss, self.loss_u, self.loss_f = self.loss_func() self.loss.backward() self.optimizer.step() self.optimizer.zero_grad() if epoch % 100 ==0: print( 'Iter %d, Loss: %.5e, Loss_u: %.5e, Loss_f: %.5e' % (epoch, self.loss.item(), self.loss_u.item(), self.loss_f.item())) # 予測 def predict(self, x, t): x = torch.tensor(x, requires_grad=True).float() t = torch.tensor(t, requires_grad=True).float() #評価モードに変更 self.dnn.eval() u = self.net_u(x, t).detach().numpy() f = self.net_f(x, t).detach().numpy() return u, f
4.4.PINNsの学習
PINNsクラスをインスタンス化し、trainメソッドを呼び出すことで学習を行います。
pinns = PINNs(t_d, t_c, x_d, x_c, y_d, 0.07)
pinns.train()
学習が進むとロスが小さくなっていきます。
Iter 0, Loss: 2.87723e-01, Loss_u: 2.87723e-01, Loss_f: 5.59655e-06 Iter 100, Loss: 8.41618e-03, Loss_u: 8.30846e-03, Loss_f: 2.15432e-01 Iter 200, Loss: 2.13162e-03, Loss_u: 1.95570e-03, Loss_f: 3.51858e-01 Iter 300, Loss: 1.81833e-03, Loss_u: 1.61931e-03, Loss_f: 3.98038e-01 Iter 400, Loss: 4.64293e-04, Loss_u: 2.53383e-04, Loss_f: 4.21820e-01 Iter 500, Loss: 3.20718e-04, Loss_u: 9.39333e-05, Loss_f: 4.53569e-01 Iter 600, Loss: 3.05332e-04, Loss_u: 7.70275e-05, Loss_f: 4.56609e-01 Iter 700, Loss: 2.78584e-04, Loss_u: 4.20533e-05, Loss_f: 4.73062e-01 Iter 800, Loss: 2.86381e-04, Loss_u: 5.40219e-05, Loss_f: 4.64719e-01 Iter 900, Loss: 3.07020e-04, Loss_u: 8.13469e-05, Loss_f: 4.51346e-01 Iter 1000, Loss: 2.70977e-04, Loss_u: 3.54998e-05, Loss_f: 4.70954e-01 Iter 1100, Loss: 3.14225e-04, Loss_u: 8.52327e-05, Loss_f: 4.57985e-01 Iter 1200, Loss: 2.64601e-04, Loss_u: 3.21115e-05, Loss_f: 4.64980e-01 Iter 1300, Loss: 2.70217e-04, Loss_u: 4.04378e-05, Loss_f: 4.59559e-01 Iter 1400, Loss: 1.53969e-03, Loss_u: 1.28447e-03, Loss_f: 5.10441e-01 Iter 1500, Loss: 2.60724e-04, Loss_u: 3.14194e-05, Loss_f: 4.58609e-01 Iter 1600, Loss: 2.54301e-04, Loss_u: 2.64207e-05, Loss_f: 4.55760e-01 Iter 1700, Loss: 2.71256e-04, Loss_u: 4.61600e-05, Loss_f: 4.50192e-01 Iter 1800, Loss: 2.79154e-04, Loss_u: 5.91911e-05, Loss_f: 4.39925e-01 Iter 1900, Loss: 2.49114e-04, Loss_u: 2.48915e-05, Loss_f: 4.48444e-01 Iter 2000, Loss: 2.55809e-04, Loss_u: 3.38683e-05, Loss_f: 4.43881e-01 Iter 2100, Loss: 2.40383e-04, Loss_u: 2.19160e-05, Loss_f: 4.36933e-01 Iter 2200, Loss: 2.52564e-04, Loss_u: 3.67999e-05, Loss_f: 4.31528e-01 Iter 2300, Loss: 2.36708e-04, Loss_u: 2.15176e-05, Loss_f: 4.30382e-01 Iter 2400, Loss: 3.19625e-04, Loss_u: 1.11283e-04, Loss_f: 4.16685e-01 ... Iter 19600, Loss: 1.65041e-06, Loss_u: 4.32224e-07, Loss_f: 2.43637e-03 Iter 19700, Loss: 2.35149e-06, Loss_u: 8.34968e-07, Loss_f: 3.03305e-03 Iter 19800, Loss: 1.78204e-06, Loss_u: 5.65130e-07, Loss_f: 2.43382e-03 Iter 19900, Loss: 2.12068e-06, Loss_u: 7.20553e-07, Loss_f: 2.80025e-03
4.5.PINNs学習済モデルの予測結果
numpyのmeshgridを使用して定義内の軸空間データを生成し、それらに対してPINNs学習済モデルで予測を行い、予測値をコンタープロットしてみます。
#予測結果の可視化 x_star = np.linspace(-1.0 , 1.0 , 100) t_star = np.linspace(0 , 1.0 , 100) X, T = np.meshgrid(x_star, t_star) X = X.reshape(-1, 1) T = T.reshape(-1, 1) u_pred, _ = pinns.predict(X, T) u_pred = u_pred.reshape(100,100).T # コンター図を作成 plt.figure(figsize=(8, 3)) plt.contourf(t_star, x_star, u_pred, 100, cmap='coolwarm') plt.colorbar() # 軸ラベルを設定 plt.scatter(t_d, x_d, marker="x", c="k") plt.xlabel("t") plt.ylabel("x") plt.show()
横軸の右に行くほど(時間が発展するほど)、コンタ値がなまっている(平滑化されている)ことがわかります。

加えて、t=0, 0.5, 1.0[s]で予測プロファイルを見てみましょう。時間発展すると波が平滑化されていることがわかります。PINNsで時間発展を解けていそうです。



4.6.解析結果との比較
解析結果とPINNsモデルの予測結果を比較してみましょう。下記のコードで有限差分法によりBurgers方程式の時間発展を解けます。
# 初期条件とパラメータの設定 L = 2 # 計算領域の長さ (-1から1までの範囲) nx = 100 # x方向の格子点数 nt = 1000 # 時間ステップ数 dt = 0.001 # 時間刻み幅 dx = L / (nx ) # x方向の格子間隔 nu = 0.07 # 粘性係数 # 初期条件の設定 x = np.linspace(-1, 1, nx) t = np.linspace(0, dt * nt, nt) u0 = -np.sin(np.pi * x) u = np.zeros((nt, nx)) u[0, :] = u0 # 数値解法のメインループ for n in range(1, nt): un = u[n - 1, :] u[n, 1:-1] = un[1:-1] - un[1:-1] * dt / (2 * dx) * (un[2:] - un[:-2]) \ + nu * dt / dx**2 * (un[2:] - 2 * un[1:-1] + un[:-2])
結果を比較してみます。

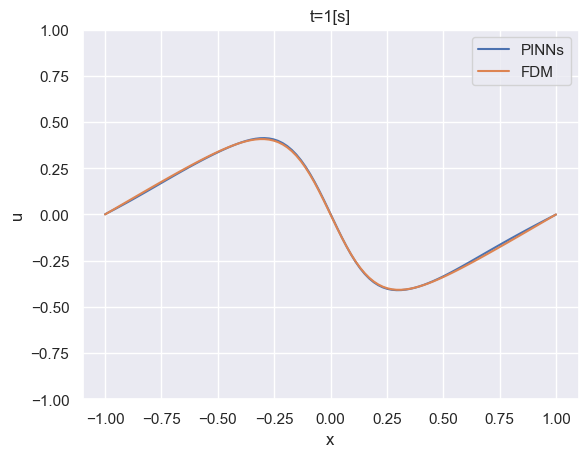
PINNsによる予測結果は解析結果をよく再現していることが確認できました。
ベイズ推論を用いたA/Bテストを行なってみる(PyMC3)


1.背景
ビジネスにおいて、異なる施策を試す場合、各施策の効果の差を検証し、意思決定を行うことが重要です。しかし、得られるデータは限られており、ばらつきが存在することが多いです。このような状況では、少数のデータのばらつきを適切に考慮しながら効果の比較を行うために、ベイズモデリングが有用です。
ベイズモデリングを使用することで、A/Bテストと呼ばれる2つの施策の効果を比較してみます。これにより、データの限定的な性質やばらつきを考慮しながら、効果の比較をより妥当な方法で行うことができます。
2.A/Bテスト
A/Bテストは、マーケティングやウェブデザインなどの領域で広く使用される実験手法です。この手法では、2つのバリエーション(AとB)を比較し、それぞれの効果や効果の差異を評価します。
マーケティングの分野では、元の施策をコントロール群(A)として、別の施策(B)を実施した時に元の施策と比べて、効果があるのかどうかを施策効果を示す評価指標を設定し、統計的手法により検証を行います。
ウェブデザインにおいては、テスト要素(タイトル、レイアウト、ボタンの色等)を選択し、テスト要素を変えたバリエーション(AとB)を用意し、ウェブサイトの訪問者数、クリック数、コンバージョン数などの指標を設定し、データを取得し、テスト要素のバリエーションによって、評価指標に違いがあるのか統計的手法により検証を行います。
3.ベイズ推論
ベイズ推論は、統計的な推論や予測を行うための強力な手法です。ベイズ推論は、ベイズの定理に基づいて確率的なモデルを構築し、データ(尤度)と事前知識を組み合わせて事後分布を推定する手法です。ベイズ推論のは以下の特徴があります。
不確実性の表現: ベイズ推論では、パラメータの事前分布や事後分布を通じて不確実性を明示的に表現することができます。これにより、データが限られている場合でも、推定結果の信頼性や不確実性を評価することが可能です。例えば、二つの異なる施策によるコンバージョン率を比較する際に、データから算出されるコンバージョン率を確率的な幅をもったものとして推定できます。これにより、推定されるコンバージョン率の信頼度も把握できます。
逐次的な更新: ベイズ推論はデータが逐次的に入手される場合にも適用することができます。新たなデータが得られるたびに、事前分布を事後分布として更新し、推定結果を更新することができます。これにより、逐次的な学習や予測が可能となります。
柔軟性と統合性: ベイズ推論は、異なるデータやモデルを柔軟に組み合わせることができます。複数のデータセットや異なるモデルを統合する際に、ベイズ推論は有用な手法となります。また、事前分布や尤度関数を自由に設定することで、モデルの複雑さやドメイン知識を組み込むことも可能です。例えば、二つの異なるコンバージョン率を比較する際に、施策によらない平均的なコンバージョン率を事前知識として設定することで、少数のサンプルしか得られず、サンプルに偏りがある際でも事前知識を活かした妥当なコンバージョン率の推定を行うことができます。
ベイズモデルの解釈: ベイズ推論によって構築されたベイズモデルは、パラメータの確率分布として表現されます。これにより、推定結果や予測結果を直感的に解釈することができます。A/Bテストにベイズ推論を導入することでt検定等の統計的検定と異なり、各群が他の群よりも優れている(劣っている)確率を直接的に算出できるメリットがあります。
4.PyMC3について
PyMC3は、ベイズ統計モデリングを行うためのPythonベースのライブラリです。PyMC3は、確率モデルの定義から事後分布の推定まで、ベイズ推論のさまざまな手法を提供します。確率変数や確率分布、尤度関数などの関数を提供しており、これらを組み合わせることで、さまざまなモデルを構築することが可能です。また、MCMC(マルコフ連鎖モンテカルロ法)等の事前分布と尤度から事後分布を計算するためのソルバーを提供しており、ベイズモデリング及びその推論が可能です。
PyMC3 Documentation — PyMC3 3.11.5 documentation
5.ベイズ推論を使用したA/Bテスト
今回は二つの異なる施策を行った時のコンバージョン率の差をベイズ推論を用いて比較してみます。
本事例では、過去のデータからコンバージョン率が平均して3%であったという事前情報を事前知識として与えます。
コンバージョン数が施行回数N, 確率pの二項分布Binominal(N, p)に従うとしてモデル化を行います。この場合、事前分布としてベータ分布を設定します。詳細には、事前知識としてpが0.03(3%)になるように(2, 98)ベータ分布に設定します。事前分布(ベータ分布)とモデル(二項分布)を用いて、MCMCにより事後分布(ベータ分布)を推定します。この事後分布からの確率的なサンプリングとして二項分布のパラメータ(=コンバージョン率)を考えることで、コンバージョン率の比較を行います。
以下に、上述したベイズモデリングを行い、事後分布のサンプリングを行うコードを記載します。
import pymc3 as pm import numpy as np # Aグループのデータ(コンバージョンの成果数とサンプル数) data_A = 10 sample_A = 200 # Bグループのデータ(コンバージョンの成果数とサンプル数) data_B = 20 sample_B = 250 #事前分布(ベータ分布のパラメータ) alpha_prior = 2 beta_prior = 98 with pm.Model() as model: # ベータ事前分布を指定 p_A = pm.Beta('p_A', alpha=alpha_prior, beta=beta_prior) p_B = pm.Beta('p_B', alpha=alpha_prior, beta=beta_prior) # ベータ分布からのデータ生成を指定 obs_A = pm.Binomial('obs_A', n=sample_A, p=p_A, observed=data_A) obs_B = pm.Binomial('obs_B', n=sample_B, p=p_B, observed=data_B) #新たな生成量として行動を起こす確率の差を定義 delta_prob = pm.Deterministic('delta_prob', p_B - p_A) # MCMCサンプリング trace = pm.sample(2000, tune=1000, cores=1) # サンプリング数: 2000, バーンイン: 1000 # 推定結果の表示 pm.summary(trace).round(2)
上記のプログラムを実行すると、コンバージョン率を比較したいA,B群の架空のコンバージョンデータを生成し、事前知識を反映させたベータ分布を事前分布、ベータ分布により決定されるパラメータpに基づく二項分布(モデル)からMCMCにより事後分布をサンプリングします。サンプリングした事後分布はtrace変数に格納されます。 以下のコードで構築したベイズモデルを可視化することができます。
pm.model_to_grahviz(model)

また、以下のコードを実行することで事後分布の可視化が行えます。
_ = pm.traceplot(trace) _ = pm.plot_posterior(trace)


続いて、以下のコードを実行することで事後分布に基づくA,B群のコンバージョン率の分布をヒストグラムで可視化します。取得データだけで平均的なコンバージョン率を計算するとそれぞれ、5%(=10/ 200)、8%(=20/ 250)となりますが、過去のデータに基づく平均的なコンバージョン率3%を事前知識として設定しているため、データのみから決まるコンバージョン率よりも小さくなっています。今回のように取得データのサンプルが小さく上振れが考えられる際に過去の事前分知識を取り込んでおくことで妥当な推定を行いやすくなります。
import matplotlib.pyplot as plt # プロット plt.hist(trace['p_A'], bins=30, density=True, alpha=0.7) plt.hist(trace['p_B'], bins=30, density=True, alpha=0.7) plt.xlabel('Conversion Rate') plt.ylabel('Density') plt.legend() plt.show()

コンバージョン率の差の分布も可視化してみます。
# AグループとBグループの差の分布をサンプリング # ヒストグラムの表示 plt.hist(trace['delta_prob'], bins=30, density=True, alpha=0.7) plt.xlabel('Difference in Conversion Rate') plt.ylabel('Density') plt.title('Difference between A and B Groups') plt.show()

最後に、A,B群とを比較して確率的にどちらが効果的か見積もってみます。
ベイズモデリングでは推定値を幅を持った値として表現するので、各群が他の群よりも優れている確率を直接的に算出できます。
(trace['p_B'] - trace['p_A'] > 0).mean() # グループBの方がグループAに比べてコンバージョン率が高いと90%の確率でいえる。







