PytorchでPINNs（Physics Informed Neural Network）を実装してみる(Burgers方程式)

1.やりたいこと

Burgers方程式に対して、PINNs(Physics Informed Neural Network)を構築し、解析解とPINNsの予測結果を比較してみます。
PINNsに関しては過去のこちらの記事を参考にしてください。

masao-ds.hatenablog.com

2.Burgers方程式

Burgers方程式は、非線形偏微分方程式の一つであり、流体力学や波動現象のモデリングに使用されます。Burgers方程式は次のように表されます。
一次元のNavier-Stokes方程式から圧力項を除いた式になっています。流体の粘性によって波が拡散し減衰していく様子を解くことができます。

3.問題設定

sin波を初期値に設定した時のBurgers方程式に基づく時間発展をPINNsを使用して予測し、有限差分法による計算結果と比較をしてみます。

4.PINNsによる解法

まず計算領域と時間発展領域を定義し、初期条件（Sin波）と境界条件（計算量領域の両端でu=0）を定義し、データを作成します。
その後、Burges方程式を満たすべき、計算領域及び時間発展領域点をいくらかサンプリングをしたデータを作成します。このサンプリングデータをを与えた時にNNモデルがBurgers方程式を満たすように（最小化するように）学習を行いつつ、初期条件や境界条件での値に対する損失を最小化するような学習モデルを定義します。

4.1.初期条件及び境界条件のデータ作成

計算領域を[-1, 1]で定義し、時間発展領域を[0, 1]sと定義します。t=0[s]での空間位置を初期のデータが存在する点としていくらか作成します（初期条件）。また、任意の時刻の境界上下端（x=-1, 1）のデータをいくらか作成します。初期に解が与えられる空間位置及び空間上下限の時刻はscipy.stats.qmcクラスを使用してランダムにサンプリングして決定します。

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

from scipy.stats import qmc
import scipy

#データの作成

#初期条件データ数
n_ic_points = 100
#上側境界条件データ数
n_bc1_points = 50
#下側境界条件データ数
n_bc2_points = 50

#scipy.stats.qmcクラスをインスタンス化(空間データと時間発展の初期及び境界データを生成するのに使用する。)
engine = qmc.LatinHypercube(d=1)

# 1[s]までの時間を乱数で生成
# 後から境界の下限と上限に割り振る。
t_d = engine.random(n=n_bc1_points + n_bc2_points)
# 初期条件なので時刻は0
temp = np.zeros([n_ic_points, 1]) 
# 初期条件と境界の時間を結合する。
t_d = np.append(temp, t_d, axis=0)

# 空間データ
# 初期の空間座標
x_d = engine.random(n=n_ic_points)
x_d = 2 * (x_d - 0.5)
# 境界の空間座標
temp1 = -1 * np.ones([n_bc1_points, 1]) # for BC1 ; x = -1
temp2 = +1 * np.ones([n_bc2_points, 1]) # for BC2 ; x = +1
# 初期条件と境界の座標を結合する。
x_d = np.append(x_d, temp1, axis=0)
x_d = np.append(x_d, temp2, axis=0)

# データポイントの可視化
plt.figure(figsize=(8, 3))
plt.scatter(t_d, x_d, marker="x", c="k")
plt.xlabel("t")
plt.ylabel("x")
plt.title("Data points (BCs & IC)")

下記が、初期にデータが与えられる空間ポイントと境界のサンプリングです。

続いて、上で作成した初期および境界の空間及び時間データに対して、uの値(教師データ)を与えます。初期条件に対しては、Sin波を与え、境界条件としては任意の時間の境界上下端に対してu=0を与えます。

# 初期条件、境界条件を設定する。

# 初期条件と境界条件で設定した空間ポイントだけ用意する。
y_d = np.zeros(x_d.shape)

# 0からn_ic_pointsは初期条件の領域
y_d[ : n_ic_points] = -np.sin(np.pi * x_d[:n_ic_points])

# 境界条件の設定
y_d[n_ic_points : n_bc1_points + n_ic_points] = 0
y_d[n_bc1_points + n_ic_points : n_bc1_points + n_ic_points + n_bc2_points] = 0

4.2.計算領域内のサンプリングデータの作成

Burgers方程式を満たしてほしい空間及び時間発展領域の点を指定した数だけランダムにサンプリングします。後に定義するPINNsモデルの中でここで定義したサンプリングデータを与えたときにBuegers方程式を満たすようにNNの学習を行います。こちらもscipy.stats.qmcクラスを使用してランダムなサンプリングを行います。

# 支配方程式を満たすべき時空間ポイント
Nc = 10000

# LHS for collocation points
engine = qmc.LatinHypercube(d=2)
data = engine.random(n=Nc)
# set x values between -1. and +1.
data[:, 1] = 2*(data[:, 1]-0.5)

# change names
t_c = np.expand_dims(data[:, 0], axis=1)
x_c = np.expand_dims(data[:, 1], axis=1)

t_c = np.vstack([t_c, t_d])
x_c = np.vstack([x_c, x_d])

# データポイントの可視化
plt.figure(figsize=(8, 3))
plt.scatter(t_c, x_c, marker="x", c="k")
plt.xlabel("t")
plt.ylabel("x")
plt.title("Data points (BCs & IC)")

サンプリング点（Burgers方程式を満たしてほしい点）が時空間領域全体で満遍なく生成できていそうです。

4.3.学習モデル定義

PINNs学習用モデルを定義します。まず、NNクラスを定義します。NNクラス内では空間位置と時間を入力すると、その空間位置と時間に対応するuの値を返すニューラルネットワークを定義しています。活性化関数にTanhを使用し、非線形変換を何層か繰り返す多層NNを作成します。このNNクラスをPINNsクラス内でインスタンス化し、NNの重みを初期や境界の教師ペアの最小化を行いつつ、サンプリングしたデータがBurgers方程式を満たすように更新(学習)して行きます。以下がNNクラスの定義コードです。

# モデル、ネットワーク定義
class NN(nn.Module):
    
    def __init__(self, n_input, n_output, neuron_per_layer=50):
        
        super(NN, self).__init__()
        
        #set activation function
        self.activation = nn.Tanh()
        
        self.n_input = n_input
        self.n_output = n_output
        
        self.affine1 = nn.Linear(self.n_input, neuron_per_layer)
        self.affine2 = nn.Linear(neuron_per_layer, neuron_per_layer)
        self.affine3 = nn.Linear(neuron_per_layer, neuron_per_layer)
        self.affine4 = nn.Linear(neuron_per_layer, neuron_per_layer)
        self.affine5 = nn.Linear(neuron_per_layer, neuron_per_layer)
        self.affine6 = nn.Linear(neuron_per_layer, neuron_per_layer)
        self.affine7 = nn.Linear(neuron_per_layer, neuron_per_layer)
        self.affine8 = nn.Linear(neuron_per_layer, self.n_output)
        
    
    def forward(self, t):
        
        t = self.activation(self.affine1(t))
        t = self.activation(self.affine2(t))
        t = self.activation(self.affine3(t))
        t = self.activation(self.affine4(t))
        t = self.activation(self.affine5(t))
        t = self.activation(self.affine6(t))
        t = self.activation(self.affine7(t))
        t = self.affine8(t)
        
        return t

続いて、PINNsクラスを定義します。
PINNsクラスは. t, x, u ：教師がある学習に使用する初期のサンプリングデータ及び境界のサンプリングデータとそれぞれt,xに対応する教師u、x_region, t_region：Burgers方程式を満たしてほしい時空間サンプリングデータのペア及びBurgers方程式のパラメータνを与えることでインスタンス化できる。
PINNsクラスは以下のメソッドを持ちます。

• net_uメソッド： 入力として受け取ったx, tのデータをconcatして一次元配列に変換し、インスタンス化されているNNクラスに入力として与え、出力（その学習時点でのuの予測値）を返します。

• net_fメソッド： x, tを入力し、自動微分により勾配の計算を行い、学習時点での支配方程式への当てはまり度合いを返します。

• loss_funcメソッド： 初期や境界条件の教師があるデータに対する損失と支配方程式への当てはまりを足し合わせて学習時の損失を定義します。

• trainメソッド： 学習を行います。

• predictメソッド： 定義域内の時空間データのペアを与えることで、学習済モデルを使用してその時空間データに対応するuの予測値を返します。

# PINNsモデルの定義
class PINNs():
    
    def __init__(self, t, t_region, x, x_region, u, nu):
        
        self.nu = nu
        
        #入力変数を定義
        #t, x : 学習に使用する初期条件及び境界条件
        #t_region, x_region:支配方程式を満たしているかどうかを評価するために使用する教師なしデータ
        #u : 学習に使用する初期条件及び境界の教師データ 
        self.t = torch.tensor(t, requires_grad=True).float()
        self.t_region = torch.tensor(t_region, requires_grad=True).float() 
        self.x = torch.tensor(x, requires_grad=True).float()
        self.x_region = torch.tensor(x_region, requires_grad=True).float()
        self.u = torch.tensor(u, requires_grad=True).float()
        
        #NNをインスタンス化
        self.dnn = NN(2, 1)
        
        #optimizers
        self.optimizer = torch.optim.Adam(self.dnn.parameters(), lr=1e-3)

    #dnnの入力にできるように空間座標と時間を結合する。
    def net_u(self, x, t):
        u = self.dnn(torch.cat([x, t], dim=1))
        return u

    #現状のエポックスでの支配方程式への当てはまりを計算
    def net_f(self, x, t):
        
        #現状のエポックスでの予測値
        u = self.net_u(x, t)
        
        #時間1階微分
        u_t = torch.autograd.grad(u, t, grad_outputs=torch.ones_like(u),retain_graph=True, create_graph=True)[0]
        #空間１階微分
        u_x = torch.autograd.grad(u, x, grad_outputs=torch.ones_like(u),retain_graph=True, create_graph=True)[0]
        #空間２回微分
        u_xx = torch.autograd.grad(u_x, x, grad_outputs=torch.ones_like(u_x),retain_graph=True, create_graph=True)[0]
        
        f = u_t + u * u_x - self.nu * u_xx 
        
        return f
    
    #損失の評価
    def loss_func(self):
            
        u_pred = self.net_u(self.x, self.t)
        f_pred = self.net_f(self.x_region, self.t_region)
        loss_u = torch.mean((self.u - u_pred)**2)
        loss_f = torch.mean(f_pred**2)
        
        loss = loss_u + loss_f*5e-4
        
        return loss, loss_u, loss_f
    
    # 学習
    def train(self):
        
        epochs = 20000
        for epoch in range(epochs):
            
            self.dnn.train()
            
            self.loss, self.loss_u, self.loss_f = self.loss_func()
            self.loss.backward()
            self.optimizer.step()
            
            self.optimizer.zero_grad()
            
            if epoch % 100 ==0:
                print( 'Iter %d, Loss: %.5e, Loss_u: %.5e, Loss_f: %.5e' % (epoch, self.loss.item(), self.loss_u.item(), self.loss_f.item()))
            
    # 予測
    def predict(self, x, t):

        x = torch.tensor(x, requires_grad=True).float()
        t = torch.tensor(t, requires_grad=True).float()
        
        #評価モードに変更
        self.dnn.eval()

        u = self.net_u(x, t).detach().numpy()
        f = self.net_f(x, t).detach().numpy()
        
        
        return u, f

4.4.PINNsの学習

PINNsクラスをインスタンス化し、trainメソッドを呼び出すことで学習を行います。

pinns = PINNs(t_d, t_c, x_d, x_c, y_d, 0.07)
pinns.train()

学習が進むとロスが小さくなっていきます。

Iter 0, Loss: 2.87723e-01, Loss_u: 2.87723e-01, Loss_f: 5.59655e-06
Iter 100, Loss: 8.41618e-03, Loss_u: 8.30846e-03, Loss_f: 2.15432e-01
Iter 200, Loss: 2.13162e-03, Loss_u: 1.95570e-03, Loss_f: 3.51858e-01
Iter 300, Loss: 1.81833e-03, Loss_u: 1.61931e-03, Loss_f: 3.98038e-01
Iter 400, Loss: 4.64293e-04, Loss_u: 2.53383e-04, Loss_f: 4.21820e-01
Iter 500, Loss: 3.20718e-04, Loss_u: 9.39333e-05, Loss_f: 4.53569e-01
Iter 600, Loss: 3.05332e-04, Loss_u: 7.70275e-05, Loss_f: 4.56609e-01
Iter 700, Loss: 2.78584e-04, Loss_u: 4.20533e-05, Loss_f: 4.73062e-01
Iter 800, Loss: 2.86381e-04, Loss_u: 5.40219e-05, Loss_f: 4.64719e-01
Iter 900, Loss: 3.07020e-04, Loss_u: 8.13469e-05, Loss_f: 4.51346e-01
Iter 1000, Loss: 2.70977e-04, Loss_u: 3.54998e-05, Loss_f: 4.70954e-01
Iter 1100, Loss: 3.14225e-04, Loss_u: 8.52327e-05, Loss_f: 4.57985e-01
Iter 1200, Loss: 2.64601e-04, Loss_u: 3.21115e-05, Loss_f: 4.64980e-01
Iter 1300, Loss: 2.70217e-04, Loss_u: 4.04378e-05, Loss_f: 4.59559e-01
Iter 1400, Loss: 1.53969e-03, Loss_u: 1.28447e-03, Loss_f: 5.10441e-01
Iter 1500, Loss: 2.60724e-04, Loss_u: 3.14194e-05, Loss_f: 4.58609e-01
Iter 1600, Loss: 2.54301e-04, Loss_u: 2.64207e-05, Loss_f: 4.55760e-01
Iter 1700, Loss: 2.71256e-04, Loss_u: 4.61600e-05, Loss_f: 4.50192e-01
Iter 1800, Loss: 2.79154e-04, Loss_u: 5.91911e-05, Loss_f: 4.39925e-01
Iter 1900, Loss: 2.49114e-04, Loss_u: 2.48915e-05, Loss_f: 4.48444e-01
Iter 2000, Loss: 2.55809e-04, Loss_u: 3.38683e-05, Loss_f: 4.43881e-01
Iter 2100, Loss: 2.40383e-04, Loss_u: 2.19160e-05, Loss_f: 4.36933e-01
Iter 2200, Loss: 2.52564e-04, Loss_u: 3.67999e-05, Loss_f: 4.31528e-01
Iter 2300, Loss: 2.36708e-04, Loss_u: 2.15176e-05, Loss_f: 4.30382e-01
Iter 2400, Loss: 3.19625e-04, Loss_u: 1.11283e-04, Loss_f: 4.16685e-01
...
Iter 19600, Loss: 1.65041e-06, Loss_u: 4.32224e-07, Loss_f: 2.43637e-03
Iter 19700, Loss: 2.35149e-06, Loss_u: 8.34968e-07, Loss_f: 3.03305e-03
Iter 19800, Loss: 1.78204e-06, Loss_u: 5.65130e-07, Loss_f: 2.43382e-03
Iter 19900, Loss: 2.12068e-06, Loss_u: 7.20553e-07, Loss_f: 2.80025e-03

4.5.PINNs学習済モデルの予測結果

numpyのmeshgridを使用して定義内の軸空間データを生成し、それらに対してPINNs学習済モデルで予測を行い、予測値をコンタープロットしてみます。

#予測結果の可視化

x_star = np.linspace(-1.0 , 1.0 , 100)
t_star = np.linspace(0 , 1.0 , 100)
X, T = np.meshgrid(x_star, t_star)

X = X.reshape(-1, 1)
T = T.reshape(-1, 1)
u_pred, _ = pinns.predict(X, T)
u_pred = u_pred.reshape(100,100).T

# コンター図を作成
plt.figure(figsize=(8, 3))
plt.contourf(t_star, x_star, u_pred, 100, cmap='coolwarm')
plt.colorbar()

# 軸ラベルを設定
plt.scatter(t_d, x_d, marker="x", c="k")
plt.xlabel("t")
plt.ylabel("x")
plt.show()

横軸の右に行くほど（時間が発展するほど）、コンタ値がなまっている（平滑化されている）ことがわかります。

加えて、t=0, 0.5, 1.0[s]で予測プロファイルを見てみましょう。時間発展すると波が平滑化されていることがわかります。PINNsで時間発展を解けていそうです。

4.6.解析結果との比較

解析結果とPINNsモデルの予測結果を比較してみましょう。下記のコードで有限差分法によりBurgers方程式の時間発展を解けます。

# 初期条件とパラメータの設定
L = 2  # 計算領域の長さ (-1から1までの範囲)
nx = 100  # x方向の格子点数
nt = 1000  # 時間ステップ数
dt = 0.001  # 時間刻み幅
dx = L / (nx )  # x方向の格子間隔
nu = 0.07  # 粘性係数

# 初期条件の設定
x = np.linspace(-1, 1, nx)
t = np.linspace(0, dt * nt, nt)
u0 = -np.sin(np.pi * x)
u = np.zeros((nt, nx))
u[0, :] = u0

# 数値解法のメインループ
for n in range(1, nt):
    un = u[n - 1, :]
    u[n, 1:-1] = un[1:-1] - un[1:-1] * dt / (2 * dx) * (un[2:] - un[:-2]) \
                 + nu * dt / dx**2 * (un[2:] - 2 * un[1:-1] + un[:-2])

結果を比較してみます。

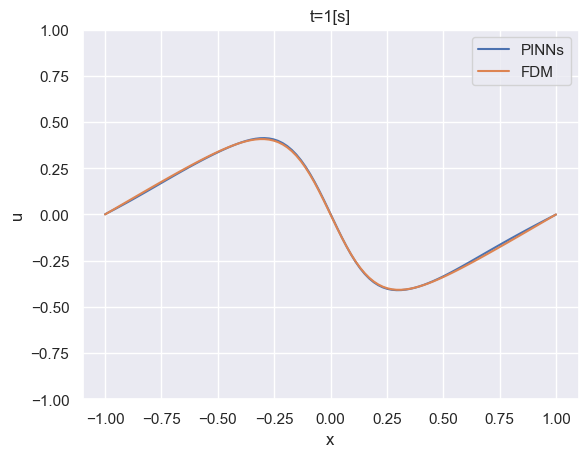
PINNsによる予測結果は解析結果をよく再現していることが確認できました。