PytorchでPINNs(Physics Informed Neural Network)を実装してみる

0.目次
1.背景
業務でPINNs(Physics Informed Neural Network)を使用したいと思い、自身で実装する方法をまとめましたので備忘録がてらまとめてみます。
2.やりたいこと
1次元の自由振動系に対して振動するマスの変位を予測するPINNsを実装し、微分方程式を解くことにより得られる解析解及びデータドリブンに学習させたNNモデルと結果を比較してみます。
3.PINNs(Physics Informed Neural Network)
3.1.PINNsとは
PINNsはPhysics Informed Neural Networkの略称で物理法則を考慮したニューラルネットワークのことです。通常のニューラルネットワークではデータドリブンで学習を行うため、学習サイクルの中で学習データをもとに予測に重要な特徴を見つけたり、特徴量を生成することが行われます。通常のニューラルネットワークでは、学習データのみを頼りにするので、学習データ数が乏しい場合、思ったような予測精度が出なかったり、過学習をしてしまったりと課題があります。学習データ以外にそのタスクに関わるドメイン知識をニューラルネットワークに与えることはできないでしょうか?
PINNsではニューラルネットワークにドメイン知識を与えることが可能です。PINNsでは予めわかっているドメイン知識(物理式、支配方程式)を学習の中に入れ込むことができます。一般的なニューラルネットワークの学習時には逐次の予測値と教師データの差分を損失として与え、この損失を誤差逆伝播法により損失に対する各重みの勾配情報を上流のネットワークに伝え、勾配に基づいて各重みを更新することで学習を行います。PINNsでは予測値と教師データの差分に加えて、物理式、支配方程式に対する損失も入れ込んで学習を行います。予め分かっている物理式を満足しているかどうかに対する正則を入れ込むことでデータが少ない場合でもデータが全くない領域に対するモデルの精度も担保できます。学習データを再現するニューラルネットワークの重みの組み合わせは複数あるが、損失が予測値と教師データの差分のみであると手元にあるデータのみに適合すればよく、学習データ領域外のデータには関心がありません。PINNsにより支配方程式を損失に入れ込むことで学習データを再現する重みの組み合わせのうちの中から学習データにはない入力条件に対する現状のニューラルネットワークの重みでの支配方程式への当てはまりを考慮しながら学習(各重みを更新)するため、学習データ領域外の条件に対しても精度が担保することができます。
PINNsの工学分野での適用シーンを考えてみます。振動工学の分野においては、振動系に対して構造物(マス)の変位を予測したり、振動の減衰の様子を把握したい場面があるかと思います。例えば、1次のマス-バネ-ダンパーの自由振動系は以下の式で表されます。
ここで
は時間、
は変位、
はバネ定数、
はダンパー係数です。
1次の振動系であれば、微分方程式を解くことで簡単に解を求めることができるが、複雑な系であれば解を求めることは難しい。PINNsを使えば、初期の計測データを用いて学習を行うことで解を容易に予測することが可能である。
流体のシミュレーションにおいては、任意の時刻の流れ場を計算(予測)する際に、計算の縮退化ができる。流体の計算には一般的に大規模な計算格子を使用し、各格子点の物理量(速度、圧力)の時間発展を繰り返し計算により求めるため計算コストが高い。PINNsを学習させることにより時刻と格子座標を入力するとその時刻の物理量を瞬時に予測することができ、計算の高速化ができる。非圧縮の流体問題では、以下のような連続の式とNavier-Stokes式をNNの損失に組み込み、初期の各格子における物理量と境界条件を与えて学習を行うことで任意の時刻の物理量(速度、圧力)を予測できるモデルが作成できる。
ここで、
は密度、
は速度ベクトル、
は時間、
は勾配(空間微分演算子)、
は圧力、
は動粘性係数、
は重力ベクトルです。
下記はPINNsの火付け役になった論文です。こちらの論文でも流体の支配方程式をPINNsを用いて解法しています。
[https://arxiv.org/pdf/1711.10561.pdf:image=https://arxiv.org/pdf/1711.10561.pdf]
3.2.自動微分
上記の具体例で見てきたように物理式、支配方程式は時空間的な偏微分項を含む偏微分方程式です。PINNsでこれらの支配方程式を学習サイクルの中で満足しているかどうかをどのように計算/評価するのでしょうか?
ニューラルネットワークの学習では損失(教師の物理量と物理量の予測値)に対する各重みの勾配情報を微分の連鎖律を使って出力側から順次計算できる仕組みを使用しています。この微分の連鎖律(自動微分という)を使用して偏微分項の計算を高速に計算できます。(ただ、ネットワークを定義した段階ではネットワーク内の重みの勾配を求めることはできますが、入力変数に対する勾配(微分項)は計算できないので、入力変数もネットワークのグラフに組み込み、微分項を計算できるようにする設定が必要になります。)Pytorchなどの深層学習用のフレームワークではDefine by Runの仕組みが実装されており、順伝播の計算をしながらネットワークをグラフとして定義し、計算過程や各ノードの出力値、勾配情報を保存しています。これにより微分の連鎖律を使用したバックワードの高速な勾配計算(自動微分)を実現しています。順伝播型の勾配計算(数値微分)では何度も同じ計算が発生して計算効率が悪いですが、自動微分では計算グラフを構築しているため、一度の順方向計算と逆方向計算で勾配を効率的に求めることができます。
PytorchでPINNsを学習させる時に支配方程式(偏微分方程式)の微分項(勾配)を求める際はpytorchのautograd.gradを使用します。autograd.gradによって算出した微分項を用いて支配方程式を組み立てます。
import torch # 変数の定義 #勾配を計算するためにrequires_grad=Trueとする。 #PINNsの入力(1次の振動系であれば時間、流体問題であれば時間と格子座標) x = torch.tensor(2.0, requires_grad=True) # 関数の定義 #PINNsの出力 #実際は関数はNNの学習の中で決まっていく(NNの出力値、予測したい物理量) def function(x): return 3*x**2 + 2*x**3 # 変数に関する勾配の計算 #torch.autograd.gradを呼び出すことでグラフが作成され、勾配を計算できる。 #予測したい物理量に対する入力の勾配値(1次の振動系であれば、マスの変位に対する時間一階微分、流体であれば流速や圧力に対する時間あるいは空間一階微分) grad_x = torch.autograd.grad(function(x), x)[0] #支配方程式 #現時点の学習段階でのNNでの支配方程式への当てはまり度 loss = grad_x + c*x + ・・・
自動微分についてはこちらの記事を参考にしてください。 pystyle.info
4.マス-バネ-ダンパー系(1次の自由振動系)
以下の1次のマス-バネ-ダンパー系に対して解析結果とNNでデータのみを学習させた場合、PINNsで学習させた場合の結果を比較する。また、本記事ではマスの質量(=m)は1とする。
初期条件:
解析解:
ここで、 は振幅、
は初期位相です。
本記事の実装は下記の記事を参考にさせていただきました。
4.1.解析解
解析解を計算します。
def analytical_solution(g, w0, t): ''' g :ダンパーの減衰係数 / (2.0 * マスの質量) -> マス質量は1.0と仮定 w0 :周波数 t :np.linespace ''' assert g <= w0 w = np.sqrt(w0**2-g**2) phi = np.arctan(-g/w) A = 1/(2*np.cos(phi)) cos = np.cos(phi+w*t) sin = np.sin(phi+w*t) exp = np.exp(-g*t) x = exp*2*A*cos return x #パラメータ g, w0 = 2, 20 c, k = 2*g, w0**2 #time t = np.linspace(0,1,100) #x_analytical x_analytical = analytical_solution(g, w0, t) x_analytical = x_analytical.reshape(-1, 1)

4.2.NNによる解法
初期の計測データのみ(5点)を用いて、以降のマスの変位を再現できるか確認してみます。
まず時間を入力してその時刻に対応するマスの変位を予測するニューラルネットワーククラス(NNクラス)を定義します。
class NN(nn.Module): def __init__(self, n_input, n_output): super(NN, self).__init__() #set activation function self.activation = nn.Tanh() self.n_input = n_input self.n_output = n_output self.affine1 = nn.Linear(self.n_input, 50) self.affine2 = nn.Linear(50, 50) self.affine3 = nn.Linear(50, 50) self.affine4 = nn.Linear(50, self.n_output) def forward(self, t): t = self.activation(self.affine1(t)) t = self.activation(self.affine2(t)) t = self.activation(self.affine3(t)) t = self.affine4(t) return t
続いて、定義したNNクラスを使用してNNの学習/予測を行うクラスを定義します。
class NN_DataDriven(): def __init__(self, t, t_region, x): self.t = torch.tensor(t, requires_grad=True).float() self.t_region = torch.tensor(t_region, requires_grad=True).float() self.x = torch.tensor(x, requires_grad=True).float() #DEfine NN self.dnn = NN(1, 1) #optimizers self.optimizer = torch.optim.Adam(self.dnn.parameters(), lr=1e-3) def loss_func(self): x_pred = self.dnn(self.t) loss = torch.mean((self.x - x_pred)**2) return loss def train(self): epochs = 10000 for epoch in range(epochs): self.dnn.train() self.loss = self.loss_func() self.loss.backward() self.optimizer.step() self.optimizer.zero_grad() if epoch % 100 ==0: print( 'Iter %d, Loss: %.5e' % (epoch, self.loss.item())) def predict(self, t): t = torch.tensor(t, requires_grad=True).float() self.dnn.eval() x = self.dnn(t) return x
作成したNN_DataDrivenクラスについて説明します。クラスインスタント時に学習に使用する教師データのペアがある入力変数tと支配方程式への適合度を算出する際に使用する学習データでない入力変数t_regionと各時刻に対する変位の教師データxをTensor型で定義する。
loss_funcメソッドでは予測値と教師データ差を損失として定義している。
trainメソッドで、学習を行い、predictメソッドで入力時刻に対する変位を予測します。
NN_DataDrivenクラスをインスタンス化して、学習を行います。
t_pinn = np.linspace(0, 1, 100) t_pinn = t_pinn.reshape(-1, 1) # Pick up random data points random_list = [0, 5, 10, 20, 30] t_data = t_pinn[random_list] x_data = x_analytical[random_list] nn_datadriven = NN_DataDriven(t_data, t_pinn, x_data) nn_datadriven.train()
学習が完了したら、predictメソッドを使用して定義域全域で変位を予測し、解析解との比較を行なってみます。
#予測 x_pred = nn_datadriven.predict(t_pinn) x_pred = x_pred.detach().numpy() #プロット #予測値 plt.plot(t_pinn, x_pred,color='orange', lw=5,label='Predict') #解析解 plt.plot(t, x_analytical, label='Analytical') #学習データ plt.scatter(t_data, x_data,s=100,label='Train') plt.xlabel('Time') plt.ylabel('Displacement') plt.legend() plt.show()
 計測データのみの学習では、初期の計測データが存在する領域では精度良く予測できていますが、学習データ以降の時間域に対しては全く予測ができておらず、過学習に陥っていることが分かります。
計測データのみの学習では、初期の計測データが存在する領域では精度良く予測できていますが、学習データ以降の時間域に対しては全く予測ができておらず、過学習に陥っていることが分かります。
4.3.PINNsによる解法
PINNsによって初期の計測データからマスの変位の時間履歴(振動の様子)を予測するモデルを作成します。
学習に使用するデータは4.2.NNによる解法の場合と同じに設定します。
まず時間を入力してその時刻に対応するマスの変位を予測するニューラルネットワーククラス(NNクラス)を定義します。
class NN(nn.Module): def __init__(self, n_input, n_output): super(NN, self).__init__() #set activation function self.activation = nn.Tanh() self.n_input = n_input self.n_output = n_output self.affine1 = nn.Linear(self.n_input, 50) self.affine2 = nn.Linear(50, 50) self.affine3 = nn.Linear(50, 50) self.affine4 = nn.Linear(50, self.n_output) def forward(self, t): t = self.activation(self.affine1(t)) t = self.activation(self.affine2(t)) t = self.activation(self.affine3(t)) t = self.affine4(t) return t
続いて、定義したNNクラスを使用してPINNsのクラスを定義します。
class PINNs(): def __init__(self, t, t_region, x, c, k): self.c = c self.k = k self.t = torch.tensor(t, requires_grad=True).float() self.t_region = torch.tensor(t_region, requires_grad=True).float() self.x = torch.tensor(x, requires_grad=True).float() #DEfine NN self.dnn = NN(1, 1) #optimizers self.optimizer = torch.optim.Adam(self.dnn.parameters(), lr=1e-3) def net_f(self, t): x = self.dnn(t) x_t = torch.autograd.grad(x, t, grad_outputs=torch.ones_like(x),retain_graph=True, create_graph=True)[0] x_tt = torch.autograd.grad(x_t, t, grad_outputs=torch.ones_like(x_t),retain_graph=True, create_graph=True)[0] f = x_tt + self.c * x_t + self.k * x return f def loss_func(self): x_pred = self.dnn(self.t) f_pred = self.net_f(self.t_region) loss_x = torch.mean((self.x - x_pred)**2) loss_f = torch.mean(f_pred**2) loss = loss_x + loss_f*5e-4 return loss, loss_x, loss_f def train(self): epochs = 50000 for epoch in range(epochs): self.dnn.train() self.loss, self.loss_x, self.loss_f = self.loss_func() self.loss.backward() self.optimizer.step() self.optimizer.zero_grad() if epoch % 100 ==0: print( 'Iter %d, Loss: %.5e, Loss_x: %.5e, Loss_f: %.5e' % (epoch, self.loss.item(), self.loss_x.item(), self.loss_f.item())) def predict(self, t): t = torch.tensor(t, requires_grad=True).float() self.dnn.eval() x = self.dnn(t) f = self.net_f(t) return x, f
作成したPINNsクラスについて説明します。クラスインスタント時に学習に使用する教師データのペアがある入力変数tと支配方程式への適合度を算出する際に使用する学習データでない入力変数t_regionと各時刻に対する変位の教師データxをTensor型で定義する。この際、勾配を計算できるようにrequires_grad=Trueとしておく。
net_fメソッドでは、touch.autograd.gradを使用して、出力変数xに対する入力変数tの時間1階及び2階微分項を算出し、支配方程式の当てはまりを評価する。
loss_funcメソッドでは、出力値と教師データの差分にnet_fメソッドで算出した支配方程式への当てはまりを加えて、ネットワーク全体の損失を定義している。出力値と教師データの差分には入力と教師のペアがあるデータセットで評価し、支配方程式への当てはまりについてはモデル定義域を分割して得られた教師データがない入力条件を与えて評価しているがポイントである。これにより、学習データに存在していない
入力条件域に対しても支配方程式の当てはまりを考慮でき、定義域全域で精度が担保できる。
trainメソッドで、学習を行い、predictメソッドで入力時刻に対する変位を予測します。
PINNsクラスをインスタンス化して、学習を行います。
#モデルの定義域を分割(学習最中のモデルの支配方程式当てはまり度を算出する際に使用する) t_pinn = np.linspace(0, 1, 100) #NNモデルに入力できる形に変換 t_pinn = t_pinn.reshape(-1, 1) #t_pinnのうちが学習に使用するデータを5点抽出 random_list = [0, 5, 10, 20, 30] t_data = t_pinn[random_list] x_data = x_analytical[random_list] #インスタンス化 pinns = PINNs(t_data, t_pinn, x_data, c, k) #学習 pinns.train()
学習イタレーションを重ねるごとに損失全体、予測値と教師データの差分が小さく、支配方程式への適合度が改善していることが確認できます。
Iter 0, Loss: 4.13146e-01, Loss_x: 3.60471e-01, Loss_f: 1.05349e+02 Iter 100, Loss: 3.71868e-01, Loss_x: 3.68585e-01, Loss_f: 6.56660e+00 Iter 200, Loss: 3.70835e-01, Loss_x: 3.66550e-01, Loss_f: 8.56958e+00 Iter 300, Loss: 3.70310e-01, Loss_x: 3.65092e-01, Loss_f: 1.04367e+01 Iter 400, Loss: 3.69086e-01, Loss_x: 3.63777e-01, Loss_f: 1.06181e+01 Iter 500, Loss: 3.65856e-01, Loss_x: 3.58496e-01, Loss_f: 1.47206e+01 Iter 600, Loss: 3.62231e-01, Loss_x: 3.53761e-01, Loss_f: 1.69404e+01 Iter 700, Loss: 3.55470e-01, Loss_x: 3.42284e-01, Loss_f: 2.63724e+01 Iter 800, Loss: 3.44797e-01, Loss_x: 3.23800e-01, Loss_f: 4.19942e+01 Iter 900, Loss: 3.30014e-01, Loss_x: 3.00918e-01, Loss_f: 5.81928e+01 Iter 1000, Loss: 3.19377e-01, Loss_x: 2.80325e-01, Loss_f: 7.81050e+01 Iter 1100, Loss: 3.06024e-01, Loss_x: 2.59271e-01, Loss_f: 9.35068e+01 Iter 1200, Loss: 2.70418e-01, Loss_x: 2.19652e-01, Loss_f: 1.01531e+02 Iter 1300, Loss: 2.46888e-01, Loss_x: 1.84986e-01, Loss_f: 1.23804e+02 Iter 1400, Loss: 2.32732e-01, Loss_x: 1.67169e-01, Loss_f: 1.31126e+02 Iter 1500, Loss: 2.21095e-01, Loss_x: 1.50208e-01, Loss_f: 1.41774e+02 Iter 1600, Loss: 2.43834e-01, Loss_x: 1.38377e-01, Loss_f: 2.10915e+02 Iter 1700, Loss: 1.99829e-01, Loss_x: 1.25502e-01, Loss_f: 1.48655e+02 Iter 1800, Loss: 1.83171e-01, Loss_x: 1.09754e-01, Loss_f: 1.46834e+02 Iter 1900, Loss: 1.68960e-01, Loss_x: 9.84287e-02, Loss_f: 1.41062e+02 Iter 2000, Loss: 1.53515e-01, Loss_x: 8.57715e-02, Loss_f: 1.35486e+02 Iter 2100, Loss: 1.39630e-01, Loss_x: 7.56336e-02, Loss_f: 1.27992e+02 Iter 2200, Loss: 1.21700e-01, Loss_x: 6.35049e-02, Loss_f: 1.16391e+02 Iter 2300, Loss: 1.04604e-01, Loss_x: 5.25336e-02, Loss_f: 1.04141e+02 Iter 2400, Loss: 8.70835e-02, Loss_x: 3.99109e-02, Loss_f: 9.43451e+01 ... Iter 23000, Loss: 9.58961e-04, Loss_x: 1.96658e-05, Loss_f: 1.87859e+00 Iter 23100, Loss: 7.20585e-04, Loss_x: 1.42954e-05, Loss_f: 1.41258e+00 Iter 23200, Loss: 7.42390e-04, Loss_x: 1.98486e-05, Loss_f: 1.44508e+00 Iter 23300, Loss: 2.59901e-03, Loss_x: 6.43220e-05, Loss_f: 5.06938e+00
学習が完了したので、predictメソッドを使用して定義域全域で変位を予測し、解析解との比較を行なってみます。
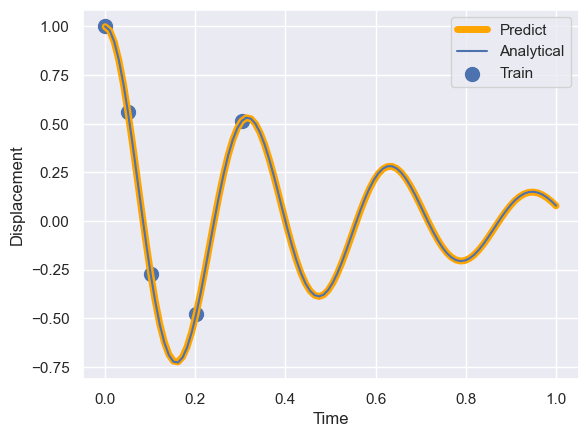
#予測 x_pred, f_pred = pinns.predict(t_pinn) x_pred = x_pred.detach().numpy() #プロット #予測値 plt.plot(t_pinn, x_pred, lw=5,label='Predict') #解析解 plt.plot(t, x_analytical, label='Analytical') #学習データ plt.scatter(t_data, x_data,s=100,label='Train') plt.xlabel('Time') plt.ylabel('Displacement') plt.legend() plt.show()

学習データがない領域に対しても高精度に予測ができています。
5.まとめ
今回、マス-バネ-ダンパーの一次の振動系に着目してpytorchを使用してPINNsを実装してみました。予め支配方程式がわかっていれば、初期の少数のサンプルで学習データ条件外の条件に対しても高精度に予測できるPINNsの強力さを体感できました。実務でもこの実装経験をいきたいと思います。